Verilen bir eşitsizliğe uyan noktalar kümesinden bahsediliyorsa, bu durumda sadece $x$ değil $y$ de işin içine girmiş demektir. Bu tür iki bilinmeyenli eşitsizliklerden birden fazla verildiğinde bir eşitsizlik sistemi verilmiş olur. Çözüm, verilen eşitsizliklerin çözümlerinin kesişimidir. [note1] tek değişkenli birden fazla eşitsizlik de bir eşitsizlik sistemidir. Ancak burada sadece çift değişkenliler için bu terimi kullanacağız [/note]
Tek değişkenli durumda $x \lt 2$ nin anlamı, reel sayılar doğrusunda $2$ den küçük bütün sayılar kümesidir. Ancak $x \lt 2$ eşitsizliğini sağlayan noktalar kümesini kartezyen düzlemde gösteriniz, dendiğinde, $x$ koordinatı bu şarta uyan tüm noktalar kümesinden bahsediliyordur. $y$ hakkında bir şart koşulmadığından $x \lt 2$ şartını sağlayan noktalar kümesi aşağıdaki gibidir. [note2] $x=2$ doğrusunun solunda kalan tüm noktaların apsisleri $2$ den küçüktür. $x=2$ üzerindeki noktaların çözüme dahil olmadığını belirtmek için kesikli çizgi kullanılır. [/note]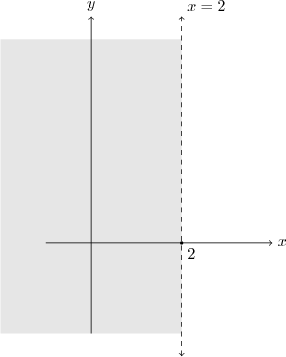
Bu bölümde bir parabol ve bir doğrunun düzlemi iki bölgeye ayırdığı eşitsizlikleri inceleyeceğiz.
Örnek
$y\leq 2x-1$ eşitsizliğinin çözüm kümesini kartezyen düzlemde gösteriniz.
Çözüm
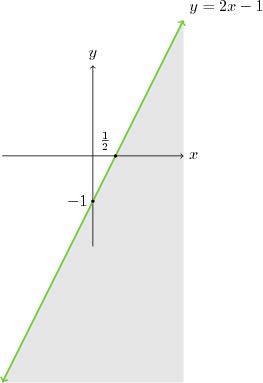
$y=2x-1$ doğrusu görüldüğü gibi düzlemi iki bölgeye ayırmaktadır. $y \lt $ ya da $y\leq $ dendiğinde doğrunun alt tarafı, $y \gt $ ya da $y\geq$ sorulduğunda da üst tarafını tarayacağız. $y\leq 2x-1$ dendiği ve eşitliğin geçerli olduğu noktalar da istendiğinden doğruyu kesikli çizgi ile değil normal çiziyoruz. [note3] $y \leq ax+b$ durumunda neden alt tarafı taradığımız anlaşılmadıysa, doğrunun üstünde bir nokta düşünelim. Bu noktanın $y$ si için $y=2x-1$ ilişkisi geçerlidir. $x$ i değiştirmeden $y$ yi küçültmek için aşağı yönlü gitmeliyiz [/note]
Örnek
$y \gt x^2-2x+1$ eşitsizliği ile verilen bölgeyi gösteriniz.
Çözüm
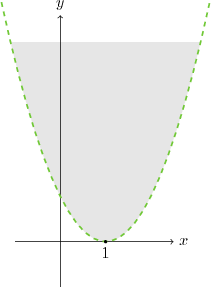
Verilen ifade bir tam karedir, $y=(x-1)^2$ ve $x=1$ noktasında $x$ eksenine teğettir.[note4] $\geq $ olmadığı için parabolü kesikli çizgilerle göstermeliyiz.[/note]
Şimdi bir eşitsizlik sistemini, yani birden fazla eşitsizliği içeren bir örneği çözelim
Örnek
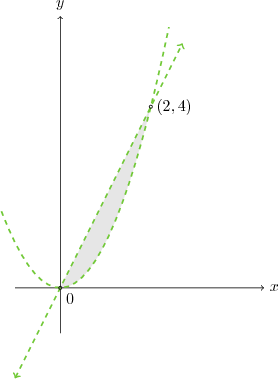
\[ y \gt x^2 \text { ve }y \lt 2x \] eşitsizlik sisteminin çözüm kümesini kartezyen düzlemde gösteriniz.
Çözüm
Hem parabolü hem de doğruyu kesikli çizgi ile çizmeliyiz. $y \gt $ dendiği için parabolün üst bölgesi ve $y \lt $ dendiği için de doğrunun alt bölgesi taranmalıdır. Doğru ve parabolün kesişim noktalarını bulalım:
\[ x^2 = 2x \Rightarrow x_1 = 0 \quad x_2 = 2 \] Bu değerleri ister doğru, ister parabol denkleminde yerine yazabiliriz, aynı $y$ değerlerini elde etmeliyiz. Kesişim noktaları $P_1 = (0,0)$ ve $P_2=(2,4)$ olmaktadır. Doğrunun alt, parabolün üstünde kalan bölge şekilde görüldüğü gibidir.