Her tabanda $\log_b 1$ in $0$ a eşit olduğu açıktır. \[ \log_b 1 = y
\Rightarrow b^y = 1 \quad y=0\]Taban $10$ ken düşünelim, bayağı logaritma fonksiyonu ile çalışalım: \[ y=\log x\]
$\log 10 = 1$ dir, $\log 100=2$ dir. $x$ büyüdükçe $y$ de büyümektedir. $\log 1=0$ dır. $1$ ile $10$ arasında bir değer koyduğumuzda da cevabın pozitif çıkacğına dikkat edelim. İçeri $1$ den küçük bir sayı koyalım, örneğin $\log \frac{1}{10}=-1$ dir. Burada ayraç $1$ dir. $1$ den büyük sayılar için cevap pozitif ve küçük sayılar için de negatif çıkmaktadır. Ancak her tabanda böyle değildir. Örneğin tabanı $1$ den küçük yapalım:
\[ \log_{\frac{1}{2}}\frac{1}{4} \]
Cevap $2$ dir. Çünkü tabanın ikinci üssü $\frac{1}{4}$ tür. $1$ den büyük sayı koyalım:
\[ \log_{\frac{1}{2}} 4 \]
Bu durumda cevap $-2$ dir, tabanın $-2$ inci kuvveti $4$ tür. Bu durumda $y=\log_b x $ fonksiyonunda $b$ ve $x$ için:
İkisi de $1$ den büyük veya ikisi de $1$ den küçükse cevap pozitif
Biri $1$ den büyükken diğeri küçükse cevap negatiftir.
Şimdi $y=\log_b x$ ve $y=b^x$ fonksiyonunun $b>1$ ve $b<1$ iken uç değerlerine bakalım. Örneğin bayağı logaritma fonksiyonu $y=\log x $ fonksiyonunda $\log 10= 1$, $\log 100 = 2$. $x$ büyüdükçe $y$ de büyüyor. $y$ çok yavaş büyüse de sınırlayan bir şey olmadığı açıktır. $x$ sonsuza giderken $y$ de sonsuza gider.
İçeri $1$ koyduğumuzu düşünelim. $\log 1=0$ ?
Not
Tüm tabanlarda $\log_b 1 = 0$ olduğu açıktır. Taban ne olursa olsun $0$ ıncı üssü $1$ dir.
Logaritmada içeri negatif veya $0$ koyamayız, ancak cevap negatif çıkabilir, örneğin içeri $\frac{1}{10}$ koyalım: $\log \frac{1}{10}= \log 10^{-1} = -1$ ya da $\log \frac{1}{1000}=\log 10^{-3}=-3$. $x$, $0$ a doğru küçüldükçe $y$ değeri de küçülmekte ve $-\infty$ a yaklaşmaktadır. $y=\ln x$ in grafiği de çok benzerdir. $x<1$ için $y$ değerleri negatiftir ve $x>1$ için pozitiftir.
$y=\log x$ in üstel karşılığı $y=10^x$ i düşünelim. Burada $x$ büyüdükçe $y$ hızla büyümekte ve $x$ küçüldükçe($-\infty$ a yaklaştıkça) $y$, $0$ a yaklaşmaktadır. Dikkat edersek bu fonksiyonlar birbirinin tersidir ve ters fonksiyonların grafikleri $y=x$ doğrusuna(I. açıortay) göre simetriktir.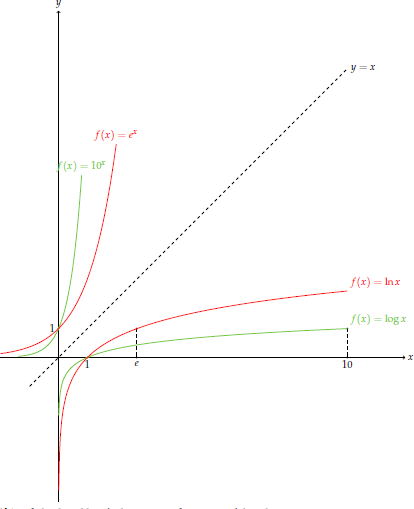 Taban $1$ den küçükken fonksiyon, $x>1$ için negatif değerler ve $x<1$ için pozitif değerler alıyordu. Örneğin $y=\log_{\frac{1}{2}} x$ grafiği aşağıdaki gibidir.
Taban $1$ den küçükken fonksiyon, $x>1$ için negatif değerler ve $x<1$ için pozitif değerler alıyordu. Örneğin $y=\log_{\frac{1}{2}} x$ grafiği aşağıdaki gibidir.
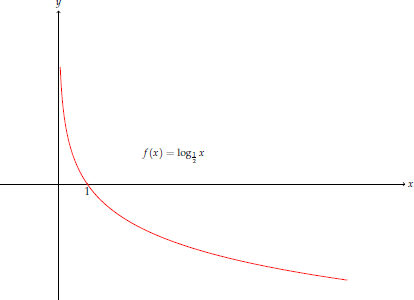 Bu grafik $\log_2 x$ grafiğinin $x$ eksenine göre simetriğidir.
Bu grafik $\log_2 x$ grafiğinin $x$ eksenine göre simetriğidir.
\[ y=\log_{\frac{1}{2}} x =\log_{2^{-1}} x = -\log_2 x \]
?
Not
Bir $f(x)$ fonksiyonu ile $-f(x)$ fonksiyonunun grafiği $x$ eksenine göre simetriktir. Aynı $x$ değerleri için bulunan $y$ değerlerinin işaretleri terstir. Tüm $(x,y)$ noktaları artık $(x,-y)$ noktalarına dönüşmüştür.
Örnek
$y=-1+\log(x-2)$ fonksiyonunun grafiğini çiziniz.
Çözüm
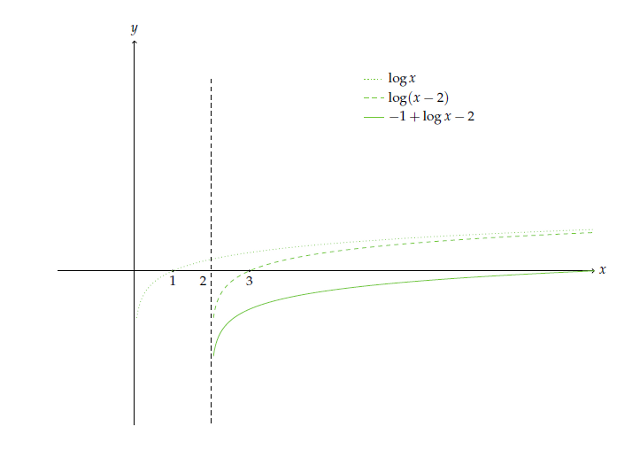
Fonksiyonu tanımsız yapan $x$ değeri düşey asimptottur. Fonksiyon $x=2$ değerine yaklaştıkça $\log(x-2)$ değeri $-\infty$ a yaklaşır. Burada adım adım öteleme yapabiliriz. $\log x$ in grafiği $2$ br sağa alındığında $\log(x-2)$, bu grafik de $1$ birim aşağı alındığında $-1+\log(x-2)$ grafiği çıkar.
?
Not
Logaritma grafiği de, genel olarak fonksiyon grafiklerindeki öteleme hareketlerine uyar. $f(x+3)$ ün grafiği $f(x)$ in $3$ birim sola kaymış halidir, $2+f(x)$ grafiği $f(x)$ in $2$ birim yukarı kaymış halidir.
Örnek
$y=2-\log_{\frac{1}{3}} (x+1)$ fonksiyonunun grafiğini çiziniz.
Çözüm
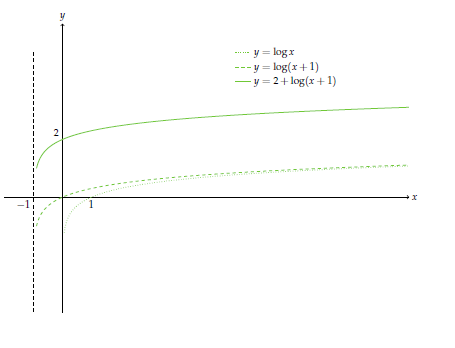
$\log_{\frac{1}{3}} (x+1) =-\log_3 (x+1)$ olduğundan soru \[y=2+\log_3 (x+1)\]
grafiğine dönüşür. Çözüm bir önceki örnekle benzerdir. $\log x$ i $1$ birim sola ötelersek $\log(x+1)$ e, bunu da $2$ br yukarı ötelersek sorulan fonksiyona ulaşırız. Düşey asimptot $x=-1$ doğrusudur.