Birinci Derece İfadeler ve İşaret Tabloları
$ax+b$ şeklindeki birinci derece ifadelerin işaret tabloları oldukça basittir. Önce ifadenin $0$ eşit olduğu yeri yani kökü bulacağız, açıkça görüldüğü gibi bu $\frac{-b}{a}$ dır. Daha sonra kökün sağ ve solunda ifadenin değerini düşüneceğiz.
Örnek
$2x-1$ ifadesinin işaret tablosunu çizin.
Çözüm
Önce kökü bulalım
\[ 2x-1=0 \Rightarrow x = \frac{1}{2} \]
Kökten daha büyük bir değer koyduğumuzda, örneğin $x=1$ için ifade pozitif, daha küçük bir değer koyduğumuzda ifade negatif olmaktadır.

Örnek
$(-x-1)(x+2) \gt 0$ eşitsizliğinin çözüm kümesi nedir?
Çözüm
İki çarpan aynı işaretli olduğunda cevap pozitif olacaktır. İkisinin de negatif ve ikisinin de pozitif olduğu yerleri görebilmek için bir tablo çizelim.
$-x-1=0 \Rightarrow x =-1$ ve $x+2=0 \Rightarrow x =-2$
Bulduğumuz kökleri küçükten büyüğe yerleştirelim ve her ifade için bir önceki örnekte olduğu gibi kökün sağ ve solunda aldığı işaretleri belirtelim. En alt satırda da iki ifadenin çarpımını gösterelim. Üstteki iki ifadenin işaretleri aynı olduğunda çarpımın işareti pozitif, farklı olduğunda negatif olacağından en alt satır tabloda görüldüğü gibidir. Kökler, çarpımın da kökleri olduğundan en alt satırda gösterilmiştir.
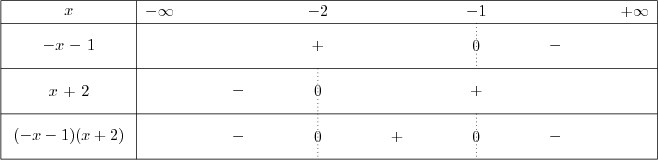
Tablodan görüldüğü gibi eşitsizliğin çözüm kümesi $(-2,-1)$ aralığıdır.[note2] Soruda $\geq$ ya da $\leq$ işaretleri kullanılsaydı, aralık kapalı olabilirdi. Bildiğimiz gibi aralığın kapalı olması uç noktaların da dahil olduğu anlamına gelmektedir.[/note]
Rasyonel ifadelerde paydanın $0$ olduğu değerlerde ifade tanımsız olduğundan kesinlikle çözüm kümesine alınamazlar ve tabloda çift çizgi ile gösterilirler.[note3] Bazen çift çizgi ileride göreceğimiz çift kat kök için de kullanılır ancak biz, tanımsız değerleri belirtmek için kullanacağız[/note]
Örnek
\[ \frac{-x(x-1)}{x+2}\leq 0\] ifadesinin çözüm kümesi nedir?
Çözüm
Burada da ayrı ayrı üç çarpan için de kök bulup tablo çizersek:
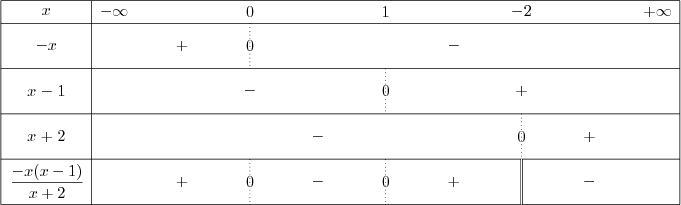
Tablodan görüldüğü gibi $\leq 0$ ı sağlayan aralıklar $[0,1]$ ve $(-2,-\infty)$ dir. $-2$ nin dahil olmadığına dikkat edelim.[note4] Çarpanların tek tek işaret tablosunu çizerek bunları en alt satırda birleştirmek yerine, alt satırı hemen çizebiliriz. Gene de, bunları tek tek yapabilmek konunun anlaşılması için önemli olduğundan bunu, ikinci derece ifadelerin işaret tablosu bölümüne bırakıyoruz [/note]
