İki karmaşık sayı arası uzaklık
Düzlemde $z=a+ib$ karmaşık sayısı $(a,b)$ noktasına karşılık geldiğine göre, iki karmaşık sayı arası uzaklık analitik geometriden bilmemiz gereken iki nokta arası uzaklık bulunuşundan başka bir şey değildir. $(x_1,y_1)$ ve $(x_2,y_2)$ noktaları arası uzaklık $d$ olmak üzere formül şu idi:
\[ d=\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} \]
Formül sadece bir pisagor içermektedir.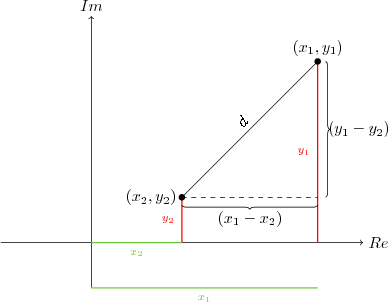
Örnek
$z_1=4-i$ ve $z_2=1+3i$ sayıları arası uzaklık nedir ?
Çözüm
$z_1$ sayısı kartezyen koordinatlarda $(4,-1)$ noktasına karşılık gelmektedir. Benzer şekilde $z_2 = (1,3)$. İki nokta arası uzaklık:
\[ |z_1z_2|= \sqrt{(4-1)^2 + (-1-3)^2 } \]
Bu da bildiğimiz $3-4-5$ üçgenidir, $|z_1z_2| = 5$
Toplama, çıkarma, çarpma ve bölmenin geometrik yorumu
* Toplama
İki karmaşık sayı toplanırken reeller ayrı sanallar ayrı toplanmaktaydı. Vektörlerde de toplama işlemi yatay ve düşey bileşenler için ayrı yapılıyordu ve bileşen vektör böyle bulunuyordu. Bir karmaşık sayıya bir vektör olarak da bakabiliriz ve toplama çıkarma aslında vektörel toplama çıkarmadır.
Örneğin $z_1=1+2i$ ve $z_2=3+i$ sayılarının toplamı olan karmaşık sayıyı bulalım.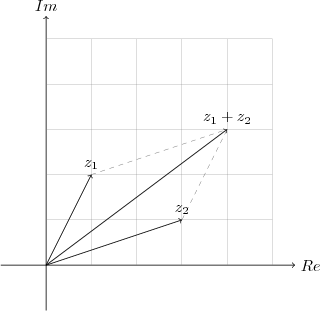
Görüldüğü gibi hem paralelkenar yöntemi hem de ucuca ekleme yöntemiyle bileşke vektörü bulabilmekteyiz.
* Çıkarma
Bir vektör $-1$ le çarpılınca hem yatay hem de düşey bileşeni yön değiştirir. Böylece şiddeti(boyu) ilk vektörle aynı ancak yönü tam ters olan bir vektör elde edilir. Vektörlerde çıkarma, aslında çıkarılan vektörün ters yönlüsü ile ilk vektörü toplamak anlamına gelir. Burada da $z_1-z_2$ işlemini hesaplarken $z_2$ yi $-1$ le çarptığımızda oluşacak vektörle $z_1$ i toplarsak çıkarma yapmış oluyoruz.
$z_1=2+i$ ve $z_2=-2+3i$ olsun. $z_1-z_2= z_1+(-z_2)$ dir.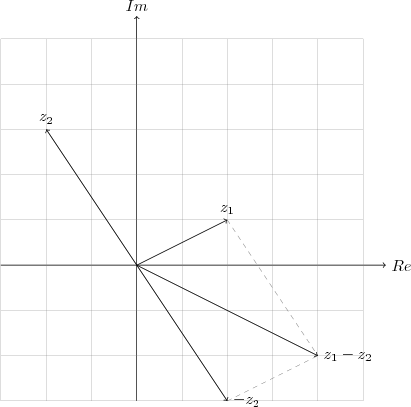
Burada önemli bir nokta geometrik olarak görünüyor. $z_1-z_2$ vektörünün boyu, $z_1$ ve $z_2$ noktaları arası uzaklıkla aynıdır.
\[ |z_1-z_2|=|z_1z_2| \]
Bunu analitik olarak da gösterebiliriz. $z_1=x_1 + iy_1$ ve $z_2 = x_2 + iy_2$ olsun:
\[ |z_1-z_2|=|(x_1 + iy_1)-(x_2 + iy_2)|=|(x_1-x_2)+(y_1-y_2)i| \]
Reel kısmı $x_1-x_2$ sanal kısmı da $y_1-y_2$ olan bir karmaşık sayı elde ettik bunun boyu da:
\[ |z_1-z_2| = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \] Bu da yukarıda incelediğimiz gibi [iki karmaşık sayı arası uzaklık](#Iki_karmasik_sayi_arasi_uzaklik_) yani $z_1z_2$ dir.
* Çarpma ve Bölme
Çarpma ve bölmenin geometrik yorumunu gözle göremiyoruz. Ancak kutupsal biçimde yaptığımız analizlerde, modüllerin çarpıldığını ve argümanların toplandığını öğrendik. Buradan anlıyoruz ki bir $z_1$ sayısı $z_2$ sayısı ile çarpılınca $z_2$ nin argümanı kadar pozitif yönde dönmekte ve modülü de $z_2$ katına çıkmaktadır. Tersini de düşünebiliriz. $z_2$ sayısı $z_1$ kadar dönmekte ve boyu da $z_1$ katına çıkmaktadır. Bir karmaşık sayının [döndürülmesi](/karmaşık-sayılar/kutupsal-biçim#Bir_karmasik_sayinin_pozitif_yoende_doendueruelmesi_) konusunda yaptığımız analiz daha geniş bir boyuta taşınmış oldu.
Bölmede de paralel şekilde, bir $z_1$ sayısı $z_2$ sayısına bölündüğünde $z_2$ nin argümanı kadar negatif yönde dönmekte ve boyu da $z_2$ nin boyuna bölünmektedir. Ancak bölmede değişme özelliği olmadığını buradan da çıkarabiliriz. $z_2$ yi $z_1$ kadar negatif yönde döndürmekle $z_1$ i $z_2$ kadar negatif yönde döndürmek aynı noktaya getirmemektedir.
Karmaşık düzlemde tek bir $z$ sayısının değil belli bir kurala uyan $z$ sayılarının da grafiğini çıkarabiliriz. Esas olarak $z=x+iy$ yazarak elde ettiğimiz denklemi düzlemde çizmeye çalışacağız.
0-|=a-denklemini-saglayan-sayilar> |z-z0 |=a denklemini sağlayan sayılar
Bu soru tipinde solda gene sorulan $z$ karmaşık sayısına bir başka sayı toplanırken, sağda sadece reel bir sayı bulunur. Elde edilen denklem bir çember denklemi olur. Neden bir çember oluştuğunu hem analitik yoldan, yani z=x+iy yazıp denklemin bizi götürdüğü yere giderek, hem de çıkarmada bulduğumuz bir sonucu buraya uygulayarak, yani $|z-z_0|$ ın $z z_0$ uzaklığı ile aynı olması ile bulacağız.
Örnek
$|z+2i-3|=4$ denklemini sağlayan karmaşık sayıları karmaşık düzlemde gösteriniz.
Çözüm
* Analitik Yol$z=x+iy$ olsun.
\begin{align*}
|z+2i-3| = |x+iy+2i-3| = 4\\
|(x-3)+(y+2)i| = 4\\
(x-3)^2 + (y+2)^2 = 4^2
\end{align*}
Son denklem, bir çember denklemidir. Merkezi $(a,b)$ ve yarıçapı $r$ olan çemberin denklemi [note1] Çemberin merkezcil denkleminin değişken $(x,y)$ noktaları ile merkez $(a,b)$ noktası uzaklığı $r$ ye eşitlediğine dikkat edelim. Çünkü çember belli bir noktaya belli uzaklıktaki noktalar kümesidir. Yani formül basit bir uzaklık formülü. [/note]
\[ (x-a)^2 + (y-b)^2 = r^2 \]
Bu durumda merkez $M(3,-2)$ ve yarıçap da $4$ birimdir.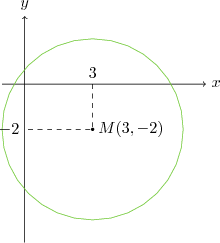
* Geometrik Yol
Şimdi olaya şöyle bakalım. Verilen eşitlik $|z-(3-2i)|$ şeklinde yazılabilir. Bu durumda ifade $z$ ile $3-2i$ karmaşık sayıları arası uzaklığı anlatır. $z_1=3-2i$ olsun:
\[ |z-z_1|= |zz_1| = 4 \]
$z_1$ zaten belli bir sayı, bu sayıdan $4$ br uzaklıktaki tüm noktalar $z$ olabilirler. Bu durumda $z_1$ merkezli ve $4$ br yarıçaplı bir çemberden bahsediyoruz. Bu da analitik yolla çok daha uzun bir şekilde bulunan grafiktir.
Örnek
$|z|=3$ denklemini sağlayan karmaşık sayıları karmaşık düzlemde gösteriniz.
Çözüm
Burada modülü $3$ olan sayılar istenmekte. Modül merkeze uzaklık olduğuna göre merkeze uzaklığı $3$ br olan noktalar kümesi isteniyor. Belli bir noktaya(merkez) belli bir uzaklıktaki(yarıçap) noktalar kümesi zaten çember demektir.
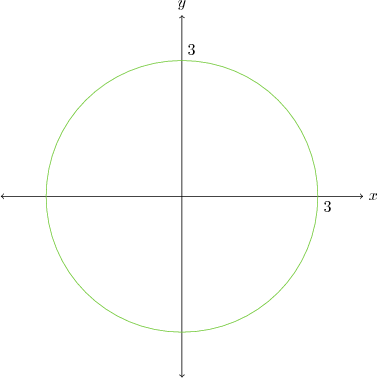
Ancak analitik yolla da yapabiliriz. $z=x+iy$ olsun.
\begin{align*}
|z|=3 \Rightarrow |x+iy| = 3 \\
x^2+y^2 =3^2
\end{align*}
Son denklem $(x-a)^2 + (y-b)^2 = r^2 $ şeklinde. $a$ ve $b$ sıfır ve $r=3$ olduğundan merkezi orijin ve yarıçapı $3$ br olan çember üzerindeki sayılar denklemi sağlarlar.
1|=|z-z2|-denklemini-saglayan-sayilar> |z-z1|=|z-z2| denklemini sağlayan sayılar
Örnek
$|z-2i+1|=|z-i-3|$ denklemini sağlayan karmaşık sayıları düzlemde gösteriniz.
Çözüm
* Analitik Yol
$z=x+iy$ olsun.
\[ |z-2i+1| = |x+iy-2i+1|=|(x+1)+(y-2)i|= \sqrt{(x+1)^2+(y-2)^2}\]
Sağ tarafta da aynı işlemi yaparsak:
\[ |z-i-3| = |x+iy-i-3|=|(x-3)+(y-1)i|= \sqrt{(x-3)^2+(y-1)^2}\]
Dolayısıyla
\begin{align*}
|z-2i+1|=|z-i-3| \Rightarrow \sqrt{(x+1)^2+(y-2)^2} = \sqrt{(x-3)^2+(y-1)^2}\\
(x+1)^2+(y-2)^2 = (x-3)^2+(y-1)^2\\
x^2+2x+1+y^2-4y+4 = x^2-6x+9+y^2-2y+1\\
8x-2y-5 =0
\end{align*}
Son çıkan ifade $ax+by+c=0$ şeklindedir ve bir doğru belirtir.
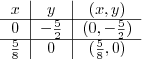
$8x-2y-5$ doğrusu $x$ eksenini $\frac{5}{8}$ de ve $y$ eksenini $-\frac{5}{2}$ de kesmektedir.
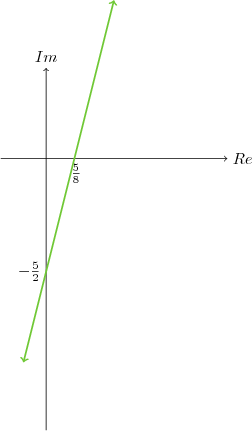
Soruda verilen karmaşık sayılar bu doğru üzerindedirler.
* Geometrik Yol
Verilen eşitlikte, iki tarafı da iki karmaşık sayının farkı olarak yazalım:
\begin{align*}
|z-2i+1| = |z-i-3|\\
|z-(-1+2i)| = |z-(3+i)|
\end{align*}
Yukarıda sol taraf $z-(-1+2i)$ nin anlamı, $(-1+2i)$ sayısı ile $z$ sayısı arası uzaklıktır. Bu uzaklık ile, aynı $z$ sayısının $3+i$ ile uzaklığının eşit olması isteniyor. İki farklı noktaya eşit uzaklıktaki noktalar kümesi de orta dikmedir. Yani burada istenen $-1+2i$ ile $3+i$ nin orta dikmesinin denklemidir.
Şekilde $P$ orta nokta ve $z$ orta dikme üzerinde alınan herhangi bir noktadır.
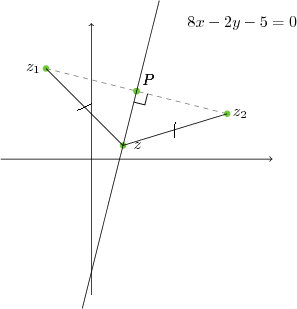
Eşitsizlik Durumları
Hem doğru hem de çember durumlarında eşitsizlik de sorulabilir. [Eşitsizlik sistemlerinden](/eşitsizlikler/eşitsizlik-sistemleri-ve-grafikleri) bildiğimiz gibi
* $y \lt ax+b$ durumunda doğrunun alt tarafı ve
* $y \gt ax+b$ durumunda doğrunun üst tarafı taranır.
$(x-a)^2 + (y-b)^2 \gt r^2$ denirse merkezi $(a,b)$ ve yarıçapı $r$ br olan çemberin dış bölgesi istenmekte, benzer şekilde küçük işareti varsa iç bölgesi istenmektedir. Tüm bu durumlarda eşitlik dahilse grafik normal, dahil değilse kesikli çizgi ile gösterilir.
Örnek
$|z-1-2i|\leq 1$ ve $|z+i-1| \gt |z+1-i|$ denklemlerini sağlayan karmaşık sayıları karmaşık düzlemde gösteriniz.
Çözüm
Eşitsizlikleri ayrı ayrı gösterip birleştirelim. $z=x+iy$ olsun.
\begin{align*}
|z-1-2i|=|x+iy-1-2i| &\leq 1\\
(x-1)^2 + (y-2)^2 &\leq 1^2
\end{align*}
Merkezi $M(1,2)$ ve yarıçapı $r=1$ br olan çemberin iç bölgesi çözümdür.
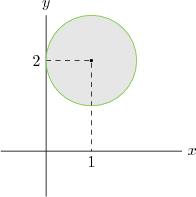
İkinci denklemde de $z=x+iy$ koyalım:
\begin{align*}
|z+i-1| &>|z+1-i| \\
|x+iy+i-1| &> |x+iy+1-i|\\
(x-1)^2+(y+1)^2 &> (x+1)^2 + (y-1)^2 \\
x^2-2x+1+y^2+2y+1 &> x^2 + 2x +1 + y^2 -2y + 1\\
-4x + 4y &>0 \\
-x + y &>0 \\
y &> x
\end{align*}
Son eşitsizlik $y=x$ doğrusunun üst tarafıdır. Eşitlik dahil olmadığı için kesikli çizgi ile çizeceğiz. İki eşitsizliğin çözüm kümesi aşağıda görülmektedir.
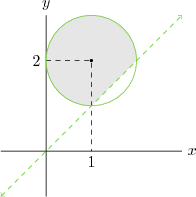
0)=a> Arg(z-z0)=a
Önce sol tarafta sadece $z$ içeren bir denklemle başlayalım:
Örnek
$\text{Arg}(z) = \frac{\pi}{6} $ denklemini sağlayan karmaşık sayıları karmaşık düzlemde gösteriniz.
Çözüm
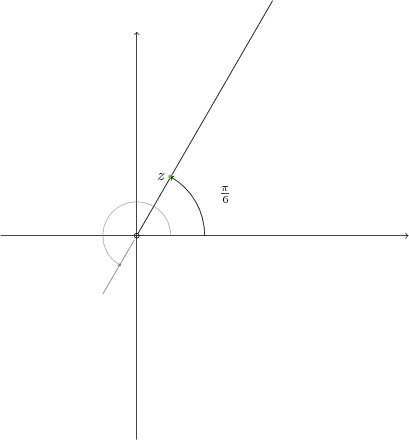
Argümanı $\frac{\pi}{6}$ olan tüm sayılar istenmektedir. Argüman, karmaşık sayıyı merkezle birleştirdiğimizde ortaya çıkan doğru parçasının, pozitif yönde yaptığı açı olduğuna göre, eğimi bu açı olan doğru üzerindeki noktalar denklemi sağlar. Ancak şekilde de görüldüğü gibi bu doğrunun birinci bölgede kalan kısmındaki noktaların argümanı $\frac{\pi}{6}$ iken üçüncü bölgedeki noktaların argümanı $\frac{7\pi}{6}$ dır. [note2] Yani doğrunun pozitif yönde yaptığı açı ile, üzerindeki noktaları merkezle birleştirdiğimizde oluşan doğru parçasının pozitif yönde yaptığı açı hep aynı değildir. Doğrunun eğimi, pozitif yönde çizilen bir yayla ilk kesiştiği noktadan ölçülür.[/note]
Ayrıca orjinin alınmadığına dikkat edelim, orjinin argümanı yoktur.
Örnek
$\text{Arg}(z-2-i)=\frac{\pi}{4}$ denklemini sağlayan karmaşık sayıları düzlemde gösteriniz.
Çözüm
$z$ nin reel kısmından $2$ ve sanal kısmından $1$ çıkarınca ortaya çıkan sayıların argümanı $\frac{\pi}{4}$ olsun isteniyor. Bu işlem $z$ yi $2$ sola ve $1$ aşağı taşıyacağından, argümanı $\frac{\pi}{4}$ olan sayıları $2$ sağa ve $1$ yukarı taşımalıyız.
\[ z-2-i=z-(2+i) \] olduğundan argümanı $\frac{\pi}{4}$ olan sayıların oluşturduğu doğruyu $2+i$ sayısına taşımalıyız. Özetle $z$ den hangi sayının çıkarıldığına bakılır ve doğru o noktadan başlatılır.
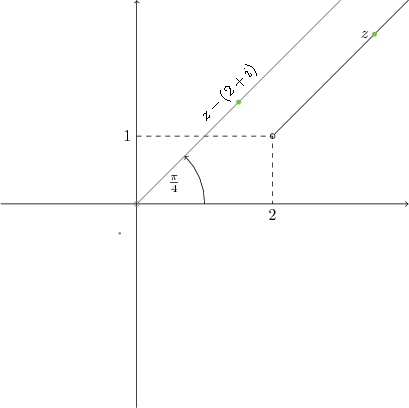
Şekilde herhangi bir $z$ sayısı seçilip $z-2-i$ işlemi sonucunda oluşan sayının, orjinden geçen ve $\frac{\pi}{4}$ açı yapan doğrunun tam üzerinde olduğu gösterilmiştir.
Burada önemli bir nokta var. Sorunun çözümü olan doğru, yani $z$ nin üzerinde olduğu doğru pozitif yönle hala $\frac{\pi}{4}$ açı yapmasına rağmen, $z$ lerin argümanları bu değildir, hatta sabit bile değildir. Çünkü argüman, karmaşık sayıyı merkezle birleştirdiğimizde ortaya çıkan doğru parçasının pozitif yönle yaptığı açıdır. Aşağıda bu nokta görülmektedir.
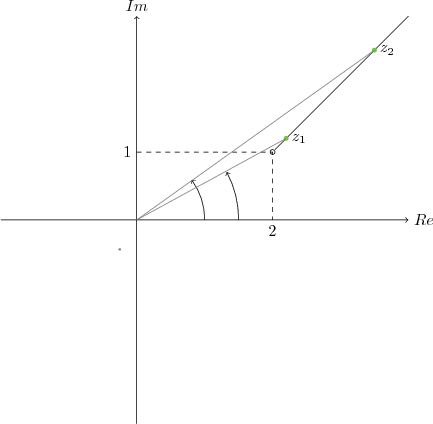
İki tane denklem verilebilir, bu durumda iki çözümün ortak kümesi (genellikle bir nokta) $z$ olur: örneğin
Örnek
$\text{Arg}(z-2)=\frac{5\pi}{6}$ ve $\text{Arg}(z+2)=\frac{\pi}{3}$ denklemlerini sağlayan $z$ sayısını bulunuz.
Çözüm
$\text{Arg}(z-2)=\frac{5\pi}{6}$ denkleminin çözümü için, önceki örneklerde de görüldüğü gibi, pozitif yönle $\frac{5\pi}{6}$ açı yapan doğruyu $(2,0)$ noktasına kaydırmalıyız. [note] Bir kez daha vurgularsak, çünkü buradan seçeceğimiz $z$ lerden $2$ çıkarırsak $2$ sola kayarlar ve bu durumda merkezle birleştiğinde $\frac{5\pi}{6}$ açı yaparlar. [/note]
Benzer şekilde $\text{Arg}(z+2)=\frac{\pi}{3}$ denklemi için de pozitif yönle $\frac{\pi}{3}$ açı yapan yarı-doğruyu $2$ sola kaydırmalıyız.
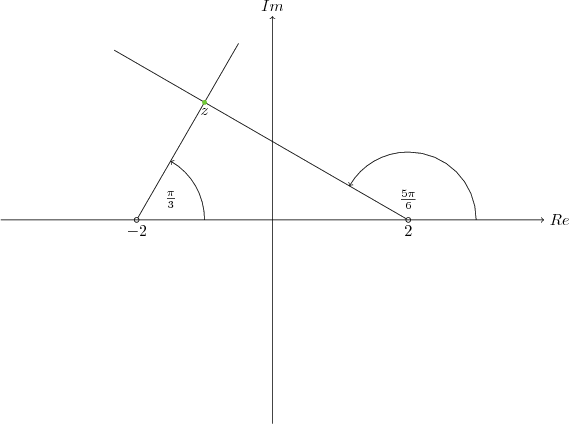
Bu iki doğrunun kesişimi şekilde gösterilen $z$ noktasıdır. Bundan sonrası basit çünkü bu bir özel üçgen. $\frac{\pi}{3}=60$ tır ve $\frac{5\pi}{6}=150$ olduğundan elimizde $30-60-90$ üçgeni var. $z$ nin koordinatları için $z$ den $x$ eksenine bir dikme inebiliriz. Bu durumda gene bir $30-60-90$ üçgeni oluşur. Gerekli hesaplar yapılınca $z=-1+\sqrt{3}i$ çıkar.
