Geometrik Yorum
İki sayının ortak katlarının en küçüğünü bulmanın geometrik anlamı bir çok sözel problemin çözümünde bize yardımcı olacaktır. Elimizde $3$ birim uzunlukta ve $4$ birim uzunlukta sayısız çubuk olduğunu düşünelim. Bize, aynı uzunluktaki çubukları yapıştırarak eşit uzunlukta iki çubuk oluşturmamız söylensin. Bu durumda dört tane $3$'lük kullanarak $12$ birim uzunluğunda bir çubuk oluşturabilir, aynı şekilde üç tane $4$ birimlik çubuğu birleştirerek gene $12$ birim uzunluğunda bir çubuk oluşturabiliriz. Bir şekille gösterirsek:

$3$'lükleri ve $4$'lükleri yanyana getirerek oluşturabileceğimiz en küçük eşit uzunluk $12$ birimdir. Bundan sonra $3$ ve $4$'ü $12$'nin tam katlarında, örneğin $24$, $36$... da birleştirebiliriz.
Bu geometrik gösterimden OKEK'in en temel problemleri kolayca anlaşılmaktadır:
Örnek
Kenarları $6$ ve $8$ birim olan dikdörtgen fayanslarla döşenebilecek en küçük kare odanın alanı ne kadardır?
Çözüm
$6$'ları yanyana getirerek ve $8$'leri yanyana getirerek kaçta birleştirebiliriz? Birinci hata bunları çarparak $48$ demek olur. Çünkü $24$'te birleştirebiliriz. İkinci hata da bize iki sayının OKEK'ini bulmak için öğretilen yanyana yazarak beraber bölme yolunu kullanmak olur. Bu yol tabii ki doğru yanıtı verir ancak amacımız şu an doğru yanıtı bulmak yanında geometrik olarak OKEK kavramını anlamak. İki sayının (tabii sayılar uygunsa) OKEK'lerini kafadan bulmak için büyük sayıyı katlayarak küçük sayının oraya ulaşıp ulaşamayacağına bakmalıyız. Örneğin $8$'in iki katı $16$'dır. $6$'nın tam bir katı ile $16$ elde edemeyiz. $8$'in üç katı $24$'tür. $6$'nın dört katı da $24$'tür. Yani OKEK'i bulduk.
Demek ki dikdörtgenleri aşağıdaki biçimde yerleştirmeliyiz.
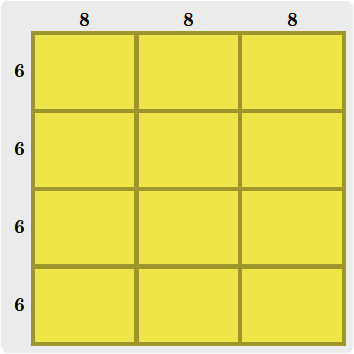
Şekilden de görüldüğü gibi en küçük boyutlu kare odanın kenarları $24$ birimdir ve alanı $24\times 24= 576$'dır.
İkinci ve çok sorulan bir örnek:
Örnek
$6$, $8$ ve $10$ dakikada bir çalan üç zil aynı anda çaldıktan kaç dakika sonra tekrar aynı anda çalarlar?
Çözüm
Bu soru da OKEK'in geometrik yorumuyla ilgilidir. Burada bu üç sayının OKEK'ini kafadan bulmak için 10 'un katlarını düşüneceğiz. Önce 10 ve 8'i kaçta birleştirebiliriz ona bakalım. 40 ikisinin de tam katıdır. Bunu bulduktan sonra 6 eğer 40'a katlanamıyorsa hemen 80'e bakmalıyız. Çünkü 8 ve 10 ancak 40 ve katlarında biraraya gelebiliyor, bunu bozmamalıyız. 6'nın tam bir katı 80 de olmamaktadır. Yani 120'ye bakmalıyız. 120'nin 6'nın bir katı olduğu açıktır. Dolayısıyla OKEK'i düşünerek bulmuş olduk: OKEK (6,8,10)=120
Ancak bu geometrik gösterimi, OKEK'in bu tip en temel soruları yanında, şu biçimde sorular için de kullanacağız:
Örnek
OKEK'leri $100$ olan iki farklı sayının toplamı en çok kaç olabilir?
Çözüm
Geometrik düşünürsek, bizden iki farklı uzunlukta çubuğu $100$'de eşitlememiz ve bunları mümkün olduğunca büyük seçmemiz istenmektedir. Çubuklardan birini $100$ birim uzunlukta seçebiliriz. Yani sayılardan biri OKEK'in kendisi olabilir. İkinci sayı en fazla $50$ olabilir. $50$ birim uzunluğunda iki çubuğu yanyana getirerek $100$ birim uzunluk elde edebiliriz.

Bir örnek daha düşünelim ancak bu sefer üç sayı istensin:
Örnek
OKEK'leri $120$ olan üç farklı sayının toplamı en fazla kaç olabilir?
Çözüm
Burada da bir sayıyı OKEK'in kendisi seçebiliriz. Yani birinci çubuğumuz $120$ birim uzunlukta. İkinci çubğun da en fazla bunun yarısı kadar olması gerektiğini bir önceki örnekte anlamıştık. Yani ikinci çubuğumuz $60$ birim uzunlukta. Üçüncü uzunluk için ilk akla gelen $60$'ın da yarısını almak yani $30$ bulmaktır. Ancak üçüncü için bundan daha büyük bir sayı seçebiliriz. Çünkü amacımız katlandığında $60$ bulmak değil $120$ bulmak. Katlandığında $120$ olabilecek üçüncü sayı $120$'yi $3$'e bölerek elde edilir ve $40$'tır. Dolayısıyla sayılarımız $120$, $60$ ve $40$. Demek ki ilk sayı için OKEK'i ikiye, ikinci sayı için üçe bölmeli ve böyle devam etmeliyiz. Yani örnekte OKEK'leri $120$ olan dört sayı istenseydi, dördüncü sayı için OKEK'i dörde bölüp $30$ bulacaktık.
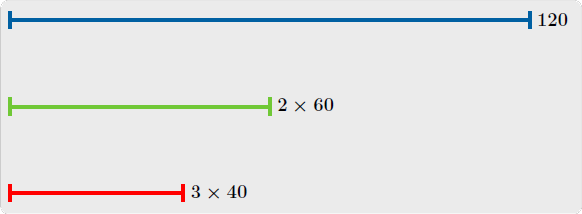
Çarpanlar Olarak OKEK
Şimdi bize ısrarla en başta öğretilen beraber bölme yönteminde neler döndüğünü anlamak için OKEK'i çarpanlar olarak düşüneceğiz. İki sayının OKEK'ini bularak yaptığımız, iki sayının da tam bir katını alarak ortak bir kata ve bunların en küçüğüne ulaşmaya çalışmaktı. Yani OKEK iki sayının da tam katıdır. Şimdi bunun çarpan olarak anlamını düşünelim. Örneğin $6$ ve $8$'in OKEK'i $24$ idi. Buna göre $24$ hem $6$'nın hem de $8$'in tam katıdır. Dolayısıyla $24$'ün içinde hem $6$ çarpan olarak bulunmalı yani $6\cdot k$ şeklinde yazılabilmeli hem de $8$ çarpan olarak bulunabilmeli yani $8\cdot l$ şeklinde de yazılabilmeli ($k,l \in \mathrm{Z}$). Yani $24$'ün çarpanları hem $6$ oluşturabilmeli hem de $8$ oluşturabilmeli.
\[ 24 = 2 \cdot 2 \cdot 2 \cdot 3 \]
Hem $6$ ve hem $8$ oluşturabilmek için gereken minimum çarpanlar bunlardır. Buradan OKEK'in bir başka bulunuş yöntemini çıkarabiliriz. Bu yöntemde bir sayı hemen OKEK'e alınır ve diğer sayıyı oluşturabilmek için gereken çarpanlar eklenir. Örneğin $12$ ve $18$'in OKEK'ini bulmak için çarpanlarına bakalım.
\[ 12 = 2\cdot 2\cdot 3 \qquad 18 = 2\cdot 3\cdot 3\]
Önce $12$'yi OKEK e alalım:\[\text{OKEK}=2\cdot 2\cdot 3 \cdots\] Daha sonra diğer sayıyı oluşturmak için neler gerekiyor bakalım. Şu an OKEK'te iki tane $2$ çarpanı var, $18$ için bir tane lazım yani $2$ eklememize gerek yok. $18$ için iki tane $3$ lazım, biz de bir tane var dolayısıyla bir tane daha $3$ koymalıyız. Yani \[ \text{OKEK}=2\cdot 2\cdot 3 \cdot 3 \]
Örnek
$a^2\cdot b \cdot c$ ve $a^3 \cdot b \cdot c^2 \cdot d$ ifadelerinin OKEK'i nedir?
Çözüm
İlk ifadeyi OKEK'e alalım: \[ \text{OKEK}=a^2 \cdot b \cdot c \cdots\] İkinci ifadede üç tane $a$ çarpanı var, OKEK'te şu an $a^2$ var, bir tane $a$ eklemeliyiz. İkinci ifadede $c^2$ var, OKEK'e bir tane $c$ eklemeliyiz. İkinci ifadede $d$ çarpanı var, OKEK'e eklemeliyiz. Dolayısıyla \[\text{OKEK}=a^3\cdot b \cdot c^2 \cdot d\]
OKEK'e çarpanlar açısından bakmayı öğrendikten sonra, OKEK'leri $100$ olan iki farklı sayının toplamının en küçük değerini bulmayı anlayabiliriz. Bu soru, daha önce çözülen toplamları en fazla olacak iki farklı sayı bulmaktan daha zor. Öncelikle OKEK'i çarpanlarına ayıralım: \[100=2^2\cdot 5^2 \] Hemen kısa yolu söyleyelim, OKEK'in çarpanları, ortak çarpan olmayacak şekilde iki sayıya dağıtılır. Yani
| I. SAYI | II. SAYI |
|---|---|
| $2^2$ | $5^2$ |
İki sayının toplamını en küçük yapan dağılım yukarıdaki gibidir. Aşağıdaki dağıtım önemli bir yanlıştır.
| I. SAYI | II. SAYI |
|---|---|
| $2$ | $2\cdot 5^2$ |
Çarpanlara bakarak OKEK bulmayı anlamışsak bunun neden yanlış olduğu açıktır. Çünkü bu durumda $\text{OKEK}=2\cdot 5^2$ olur. Değişik soru tiplerini yapabilmek için şimdi de OKEK'leri $100$ olabilecek başka sayı ikilileri de yazmaya çalışalım. Toplamlarını en küçük yapmamız gerekmediği için ortak çarpan olacak şekilde dağıtabiliriz. Örneğin:
| I. SAYI | II. SAYI |
|---|---|
| $2^2$ | $2\cdot 5^2$ |
| $2^2\cdot 5$ | $5^2$ |
| $2\cdot 5$ | $2^2 \cdot 5^2$ |
Örneğin birinci satırda, II. sayıya bir $2$ çarpanı koyduk, bunun OKEK açısından bir anlamı yok, çünkü nasılsa I. sayıda $2^2$ bulunduğu için OKEK'e $2^2$ koyacağız.
Örnek
$24$, $36$ ve $x$ sayılarının OKEK'i $720$ ise $x$ en az kaç olabilir?
Çözüm
OKEK'i çarpanlarına ayıralım: \[ \text{OKEK}=2^4\cdot 3^2 \cdot 5 \] Bu çarpanları OKEK'e koymak zorunda olmalıyız. Verilen sayıları da çarpanlarına ayıralım:
| I. SAYI | II. SAYI | III. SAYI |
|---|---|---|
| $2^3\cdot 3 $ | $2^2 \cdot 3^2$ | $x$ |
İlk iki sayının OKEK'ini bulalım: \[ \text{OKEK}=2^3\cdot 3^2 \] iki sayının da çarpanlarını içeren minimum sayı budur. Verilen OKEK'te dört tane $2$ çarpanı ve $5$ var. Bu çarpanları da içerecek şekilde OKEK'i genişletmemiz için $x=2^4\cdot 5$ olmalıdır. \[x=80\]
OKEK ve Bölünebilme
İki sayının(veya daha fazla) OKEK'i, onları oluşturan çarpanları içereceğinden ve bu çarpanları içeren en küçük sayı olduğundan, OKEK, bu iki sayıya da bölünen en küçük sayıdır. Yani $4$ ve $6$'nın OKEK'i $12$'dir ve $4$ ve $6$'ya bölünebilen en küçük pozitif tam sayı da $12$'dir. $4$ ve $6$'ya aynı anda bölünen diğer sayılar $24$, $36$ ... diye devam eder ve $12$'nin katı olmak zorundadırlar.
Şimdi hem $6$'ya hem $8$'e bölündüğünde $2$ kalanını verecek pozitif sayılar bulmaya çalışalım. Öncelikle bu kalanı verecek en küçük pozitif tam sayı, biraz garip gelecek ancak $2$'dir. $2$, $6$'ya bölünür, bölüm $0$'dır ve kalan da $2$'dir. Tabii ki amacımız $6$ ve $8$'den daha büyük sayılar bulmaya çalışmak ancak bazen böyle önemsiz şaşırtmalar test sorularında çıkmaktadır.
Önce $6$ ve $8$'e bölünebilen en küçük pozitif sayıyı bulalım: \[\text{OKEK}=24\]
$24$, hem $6$'lıklara ayrılabilir hem de $8$'liklere ayrılabilir en küçük pozitif sayıdır.
\[ 24 = 6 + 6 + 6+ 6 \] \[24 = 8 + 8 + 8 \] $24$'e bir eklersek hem $8$'e hem de $6$'ya bölündüğünde $1$ kalanını verir.
\[ 25 = 6 + 6 + 6+ 6 + 1 \] \[24 = 8 + 8 + 8 + 1 \]
$6$ ve $8$'e bölündüğünde $1$ kalanını veren sayıları bulmak için OKEK'in katlarını almalı ve bir eklemeliyiz. $25$'ten sonraki sayı $24\cdot 2 + 1 $
Örnek
$4$ ve $9$'a bölündüğünde $2$ kalanını veren $100$'den küçük en büyük sayı nedir?
Çözüm
\[\text{OKEK}(4,9)=36\] $36$'nın katlarını alıp $2$ eklersek $4$ ve $9$'a bölündüğünde $2$ kalanını veren sayılar elde ederiz. $36$'nın $100$'e en yakın katı $36 \cdot 2 = 72$'dir. Dolayısıyla aradığımız sayı \[ 72 + 2 = 74\]
Bu sorunun başka bir ifadesi de şudur:
Örnek
\[ A = 3x+1=4y+1=5z+1 \text{ ve}\qquad x,y,z \in \mathrm{Z^+} \] olduğuna göre $A$'nın $200$'den küçük en büyük değeri için $x+y+z$ toplamı nedir?
Çözüm
$x,y \text{ ve } z$ tam sayı olduğundan $A$ sayısı $3$'ün, $4$'ün ve $5$'in bir tam katından bir fazladır. Dolayısıyla $3$'e, $4$'e ve $5$'e bölündüğünde $1$ kalanını verir. \[ \text{OKEK}(3,4,5)=60 \] OKEK'in tam katlarına $1$ ekleyerek şartları sağlayan $A$ sayılarını bulabiliriz. $200$'den küçük bir $A$ sayısı istendiğinden \[ A=3\cdot 60 + 1=181 \]
$A=181$ için $x,y \text{ ve } z$ değerlerini hesaplamalıyız.
\[ 181 = 3x+1=4y+1=5z+1 \] \[ x= 60 \quad y = 45 \quad \text{ ve } z= 36 \] çıkar.
Bu soruyu daha teorik bir şekilde çözmek için her taraftan bir çıkarılır: \[ A-1 = 3x=4y=5z \] Dolayısıyla $A-1$ sayısı hem $3$, hem $4$ ve hem de $5$'in bir tam katıdır. Yani bu sayıların OKEK'lerinin tam bir katıdır.
\[ A-1 = \text{OKEK}(3,4,5)\cdot k \] Buradan $k=3$ için $A$'nın $200$'den küçük en büyük değeri elde edilir.
Yukarıdaki soru ile şimdi çözeceğimiz örnek de özünde aynıdır.
Örnek
\[ A = 3x-2=4y+9=5z-9 \text{ ve}\qquad x,y,z \in \mathrm{Z^+} \]
Çözüm
$x$ tam sayı ise $3x-2$ şeklindeki sayılar $3$'e bölündüğünde $1$ kalanını verirler.
Bunu hızlıca yapmak için $ax+b$ şeklinde verilen bir ifadede $b$ negatif ise pozitif olana kadar $a$ eklenir. Örneğin burada $-2$ negatif, pozitif olana kadar $3$ eklemeliyiz, bir tane eklediğimiz an $+1$ olur.
Gene $5z-9$ ifadesinde $-9$ negatif olduğundan pozitif olana kadar $5$ eklenir, iki tane $5$ eklediğimizde $+1$ olur.
Eğer $ax+b$ şeklinde verildiğinde, $b$ negatif değil de büyük bir pozitif sayı ise en küçük pozitif tam sayı olana kadar $a$ çıkarılır. Örneğin $4y+9$'da $9$'dan iki tane $4$ çıkarıp $+1$ haline çevirmeliyiz. Uzun görünse de bunlar bu soru tipinin kafadan hızlı çözülmesi için gerekli becerilerdir.
Teorik bir çözüm şöyledir:\[ A = 3 \cdot (x-1) + 1 = 4\cdot (y+2)+1 = 5 \cdot (z-2) + 1 \] Burada $x, y \text{ ve } z \in \mathrm{Z^+}$ olduğundan $(x-1), (y+2) \text{ ve } (z-2) \in \mathrm{Z}$ olur.
\[ A-1 = 3 \cdot (x-1) = 4\cdot (y+2) = 5 \cdot (z-2) \]
Gene bir önceki daha basit örnekte olduğu gibi $A-1$ sayısı $3,4 \text{ ve } 5$'in tam bir katıdır.
\[ A-1 = \text{OKEK}(3,4,5)\cdot k \] Burada $k$ gene $3$'tür ve $A$ değeri de aynıdır ancak $x, y \text{ ve } z$ değerlerinin değiştiğine dikkat edelim.
\[ 181 = 3x-2=4y+9=5z-9 \] \[ x= 61 \quad y = 43 \quad \text{ ve } z= 38 \]
Şimdi kalanın aynı olmadığı tipik bir soru düşünelim. Örneğin $4$'e bölündüğünde $1$ ve $6$'ya bölündüğünde $3$ kalanını verecek pozitif sayılar oluşturmaya çalışalım. Bu soru tipinde bölenle kalan farkı aynıdır. Örneğin bölen $4$ ve kalan $1$ isteniyor, fark $3$'tür, bölen $6$ ve kalan $3$ isteniyor gene farkları $3$'tür. İstenen sayılar, OKEK'in tam katlarından bu fark çıkarılarak bulunur. $4$ ve $6$'nın OKEK'i $12$'dir. İstenen ilk sayı $12-3=9$'dur. $9$, dörde bölününce bir kalanını ve $6$'ya bölününce $3$ kalanını veren ilk pozitif tam sayıdır. Sonraki sayılar için önce OKEK'i katlamalı ve sonra $3$ çıkarmalıyız:
Sonraki sayı $2\cdot 12 -3 = 21$, bir sonraki $3\cdot 12 - 3=33$ ...
Örnek
$6$'ya bölündüğünde $1$, $8$'e bölündüğünde $3$ kalanını veren $95$'ten küçük en büyük sayı nedir?
Çözüm
Verilen bölenlerle istenen kalanlar farkı $5$'tir. $\text{OKEK}(6,8)=24$ olduğundan $24$'ün katlarından $5$ çıkarırsak istenen kalanları elde ederiz. OKEK'in $4$ katı $96$'dır. $96-5=91$ istenen şartları sağlar. Bu soruda yapılan tipik bir hata, $4$ katı $95$'i geçtiğinden, OKEK'in $3$ katını alıp $5$ çıkarmaktır. Ancak $96$ istenen sınırdan büyükse de $5$ çıkaracağımız için sayı $95$'ten küçük olmaktadır.
Bu soru tipinin de sözel olmayan versiyonu şudur:
\[ A = 6x+1 = 8y+3 \qquad \text{ ve } x,y \in \mathrm{Z^+} \] olduğuna göre $95$'ten küçük en büyük $A$ değeri nedir?
Sorunun aşağıdaki versiyonunun $A$ değerini değiştirmeyeceğine ancak $x$ ve $y$ değerlerini değiştireceğine dikkat edelim:
\[ A = 6x-11 = 8y+11 \qquad \text{ ve } x,y\in \mathrm{Z^+} \] olduğuna göre $95$'ten küçük en büyük $A$ değeri nedir?
OBEB
İki sayının ortak bölenlerinin en büyüğü, ikisini de tam bölen en büyük pozitif sayıdır. Tipik OBEB problemlerinden bir kaç tane çözdükten sonra OKEK ve OBEB'in beraber kullanıldığı problemlere geçebiliriz.
Örnek
$20$ kilo pirinç, $28$ kilo bulgur ve $32$ kilo un, ayrı ayrı hiç artmayacak şekilde eşit ağırlıkta paketlere bölünecektir. En az kaç paket gerekir?
Çözüm
Üç sayıyı da bölebileceğimiz en büyük sayıyı bulalım:
| I.SAYI | II.SAYI | III.SAYI | Bölen |
|---|---|---|---|
| $20$ | $28$ | $32$ | $2$ |
| $10$ | $14$ | $16$ | $2$ |
| $5$ | $7$ | $8$ |
Bölmeye devam etmemize gerek yok, çünkü ortak bölen kalmadı. $\text{OBEB}=4$ olduğuna göre paketlerimiz $4$'er kiloluk olmalıdır. $20$ kilo pirinç $4$ kiloluk paketlere bölünürse $5$ paket, $28$ kilo bulgur $7$ paket ve $32$ kilo un $8$ paket eder. Dolayısıyla $20$ paket gerekmektedir. OBEB bulurken bölmeyi bıraktığımızda elimizdeki son satırın $5\quad 7\quad 8$, zaten $20$, $28$ ve $32$'nin $4$'e bölünmüş halleri olduğuna dikkat edelim.
Bölen yerine çarpan da diyebiliriz. İki sayının EBOB'u, bu iki sayıda da ortak bulunan tüm çarpanlardır. Örneğin EBOB'ları $10$ olan iki sayı dendiğinde
| I.SAYI | II.SAYI |
|---|---|
| $10\cdot a$ | $10 \cdot b$ |
yazabiliriz, ayrıca $a$ ve $b$'nin ortak bölenleri olamayacağını (aralarında asallar) da biliyoruz, çünkü bu durumda $\text{OBEB}=10$ olamaz.
Örnek
$86$'yı böldüğünde $6$ ve $122$'yi böldüğünde $2$ kalanını veren en büyük tamsayı nedir?
Çözüm
$86$'yı böldüğünde $6$ kalanını veren sayı, $80$'i böldüğünde kalan vermez. Aynı şekilde, $122$'yi böldüğünde $2$ kalanını veren sayı $120$'yi tam bölmektedir. $80$'i ve $120$'yi tam bölen en büyük sayı istenmektedir.
\[ \text{OBEB}(80,120)=40\] $40$ sayısı istenen şartları sağlar.
Örnek
Kenarları $80$ ve $100$ metre olan dikdörtgen şeklindeki bir arsanın çevresine eşit aralıklarla ağaçlar dikilecektir. Köşelere birer ağaç dikilmek şartıyla en az kaç ağaç dikilebilir?
Çözüm
Bu soru da, arsa kenarlarının OBEB'ini alarak çözülmektedir. \[ \text{OBEB}(80,100)=20 \] olduğundan ağaçlar $20$ metre aralıklarla dikilmelidir. Tüm çevre $360$ metredir. $360$'ı $20$'ye bölersek $18$ buluruz.
Bu sorunun çözümünü tam anlamak, buna benzeyen daha zor soruların çözülmesinde de önemlidir.
$80$ metrelik bir uzunluğu $20$ metrelik aralıklara bölmek için ağaç dikersek dört değil beş ağaç kullanmamız gerekir. Aynı şekilde $120$ metrelik bir uzunluğa başta ve sonda ağaç olacak şekilde $20$ metre aralıklarla ağaç dikersek toplam $7$ ağaç dikmiş oluruz. Ancak arsamız dikdörtgen olduğundan $80$ metrelik kenar $120$ metrelik kenarla köşeleri paylaştığından bu fazlalıklar yok olmaktadır. Dikdörtgeni açarak düz bir çizgi haline getirirsek arsanın çevresi kadar bir çizgi elde ederiz. Bu çizgiye $20$ metre aralıklarla ağaç dikersek toplam $19$ ağaç kullanmalıyız. Ancak baştaki ve sondaki ağaçlar, şekil kapalı olduğundan aslında aynıdır, dolayısıyla $18$ ağaç gerekmektedir.
Çözümlü Örnekler
Örnek
OKEK'leri $120$ ve OBEB'leri $8$ olan iki sayının çarpımı kaçtır?Çözüm
Bunun nedenini düşünelim:
OBEB'leri $8$ olduğundan iki sayıya da bu çarpanı koymak zorundayız.
| I.SAYI | II.SAYI |
|---|---|
| $8\cdot x$ | $8\cdot y$ |
Daha önce açıkladığımız gibi $x$ ve $y$ arasında ortak çarpan olamaz, çünkü bu durumda OBEB $8$'den daha büyük olur. OKEK bulmak için birinci sayıyı alıp ikinci sayıda olmayan çarpanları eklersek \[\text{OKEK}=8\cdot x \cdot y \]
$a$ ve $b$'nin çarpımı \[ a\cdot b = \underbrace{8}_{OBEB}\cdot \underbrace {x \cdot 8y}_{OKEK} \] OKEK ve OBEB'in çarpımıdır.
Örnek
$a$ ve $b$ ardışık tek sayılardır. \[ \text{OKEK}(a,b)-\text{OBEB}(a,b)=142 \] ise $a+b$ nedir?Çözüm
Örnek
Dairesel bir pist etrafında koşan üç koşucudan birincisi bir turu $10$, ikincisi $15$ ve üçüncüsü $20$ dakikada tamamlamaktadır. Aynı noktadan aynı anda aynı yöne koşmaya başlıyorlar. Tekrar aynı yerde buluştuklarında en hızlı koşucu kaç tur atmış olur?
Çözüm
\[ \text{OKEK}(10,15,20)=60 \] olduğundan $60$ dakikada bir aynı yere gelirler. En hızlı olan, bir turu $10$ dakikada bitirendir. Dolayısıyla $60 \div 10 = 6$ tur atmış olur.
Örnek
Bir torbadaki bilyeler $5$ erli ve $8$ erli paketlendiğinde $3$ bilye artıyor. $9$ arlı paketlendiğinde ise hiç bilye artmıyor. Torbadaki bilyelerin sayısı $150$'den fazla ve $250$'den az ise bilyelerin sayısının rakamları toplamı nedir?
Çözüm
Öncelikle $5$'e ve $8$'e bölündüğünde $3$ kalanını veren sayılar üretelim.
\[ \text{OKEK}(5,8)\cdot k + 3 = 40 \cdot k +3 \] Aralık dar olduğundan deneyebiliriz. $40$'ın $150$'den büyük ilk katı $160$'tır. Demek ki ilk sayımız $163$, ikincisi $203$, üçüncüsü de $243$'tür. Bu sayılardan $243$ dokuza tam bölünür.
Örnek
$\text{OKEK}(a,b)=90$ ve $3a=5b$ ise $\text{OBEB}(a,b)$ nedir?
Çözüm
$3a = 5b$ eşitliğinden $a=5k$ ve $b=3k$ yazabiliriz.
| $a$ | $b$ |
|---|---|
| $5k$ | $3k$ |
OKEK bulmak için birinci sayıyı alalım ve ikinci sayıda olup bizde olmayan sayıları ekleyelim.
\[ \text{OKEK}(a,b)=5k \cdot 3 =15k \]
Buradan $15k=90$ ve $k=6$ çıkar. $k$, tablodan görüldüğü gibi bu iki sayının OBEB'idir.
Örnek
$m$ ve $n$ pozitif tam sayılarının ortak bölenlerinin en büyüğü $\text{OBEB}(m,n) = 6$ ve ortak katlarının en küçüğü OKEK(m,n)$=60$ tır.
$m+n =42$ olduğuna göre, $|m-n|$ kaçtır? (2007-ÖSS-1)
Çözüm
$\text{OBEB}(m,n)=6$ olduğundan ikisine de bu çarpanı koyalım.
| $m$ | $n$ |
|---|---|
| $6\cdot a$ | $6 \cdot b$ |
$\text{OKEK}(m,n) = 6 \cdot a \cdot b = 60$ olur. Buradan $a \cdot b =10$ çıkar. $m+n$ toplamını $42$ yapmak için $a=2$ ve $b=5$ seçmeliyiz. Buradan \[ m=12 \quad n = 30 \qquad \text{ ve } |m-n| = 18 \]
Örnek
Eni $81$ metre, boyu $270$ metre olan dikdörtgen biçimindeki bir tarla, hiç alan artmayacak biçimde eş karelere bölünerek küçük bahçeler yapılıyor.
Bu şekilde en az kaç tane eş bahçe elde edilir?
Çözüm
$81$ ve $270$'in OBEB'i
| I.SAYI | II.SAYI | Bölen |
|---|---|---|
| $81$ | $270$ | $9$ |
| $9$ | $30$ | $3$ |
| $3$ | $10$ |
OBEB bulurken hemen ilk görülen ortak sayıya böldük ve ortak bölen kalmayınca devam etmedik.
\[ OBEB(81,270) = 27 \] olduğundan bahçe, $27$ metre kenarları olan karelere bölünebilir.
$81\div 27 =3 $ ve $270 \div 27 = 10$
(OBEB bulurken son satır $3 \quad 10$ bölümleri vermektedir)
\[ 3\cdot 10 = 30 \] bahçe elde edilir.
Örnek
$a$ ve $b$ doğal sayıları için \[ OBEB(a,b)=4 \text{ ve } a^2-b^2= 528 \] olduğuna göre $a+b$ toplamının en küçük değeri nedir?
Çözüm
OBEB ikisinde de ortak bulunan çarpanlardır.
| $a$ | $b$ |
|---|---|
| $4 \cdot k$ | $4 \cdot m$ |
\[ a^2-b^2 = (4k)^2 - (4m)^2 = 16 (k^2-m^2)=528 \]
Buradan $k^2-m^2 = 33$ çıkmaktadır.
Çarpanlara ayırırsak \[ (k-m)\cdot (k+m) = 33 \]
$(k-m)=3$ ve $(k+m)=11$ alırsak en küçük $x$ ve $y$ değerlerini elde edeceğiz. En küçük sorulmasaydı $(k+m)=33$ ve $(k-m)=1$ i de alabilirdik.
\begin{align*}
(k-m)=& 3 \\
(k+m)=& 11 \\
2k =& 14 \\
k=& 7 \\
\end{align*}
Bir denklemde yerine yazarsak $m=4$ olur. Bu değerlerle \[ a=28 \quad \text{ ve } \quad b = 16 \] bulunur.
Örnek
OBEB(a,b)=12, OKEK}(a,b)=360 ve $ x \lt y $ olduğuna göre, $x$'in alabileceği kaç farklı değer vardır?
Çözüm
Önce OBEB i ikisine de koyalım.
| $ x $ | $y$ |
|---|---|
| $12 \cdot a$ | $12 \cdot b$ |
OKEK in $12\cdot a \cdot b$ olduğunu biliyoruz. Dolayısıyla \[ a\cdot b= 30 \]
\( x \lt y \) olduğundan $ a \lt b$ olacak şekilde $30$ u çarpanlarına ayırabiliriz.
| $a$ | $b$ |
|---|---|
| $1$ | $30$ |
| $2$ | $15$ |
| $3$ | $10$ |
| $5$ | $6$ |
Beş farklı $a$ değeri olduğundan beş farklı $x$ değeri vardır.
