Sabit bir sayı ile 2. dereceden bir denklemin köklerinin karşılaştırılması
Bir ikinci derece denklemin kökleri ile herhangi bir $k$ reel sayısı arasındaki ilişkiyi iki bölümde inceleyeceğiz,
* $k=0$
* $k\neq 0$.
İnceleyeceğimiz ilişki $k$ sayısının iki kökten de küçük, ortada ya da ikisinden de büyük olup olmadığıdır. [note] Sıralama ilişkileri reel sayılar arasında geçerli olduğundan, köklerin pozitifliği, negatifliği veya bir reel sayıdan büyük ya da küçük oluşları ile ilgili bir ilişki köklerin de reel olduğu anlamına gelir. Yani aşağıda incelenen durumlarda $\Delta \geq 0$ şartı mutlaka sağlanmalıdır[/note]
* $k=0$ durumu, ikinci derece denklemlerde öğrendiğimiz kökler çarpımı/toplamı ve katsayılar arasındaki ilişkilerle kolayca anlaşılacaktır.
\[ ax^2 + bx + c \] denkleminin kökleri $x_1$ ve $x_2$ ise \[ x_1+ x_2 = -\frac{b}{a} \qquad x_1 x_2 = \frac{c}{a} \]
* $k=0$
Toplam üç ihtimal var. İki kök de $0$ dan küçüktür. Biri $0$ dan küçük biri büyüktür ve ikisi de $0$ dan büyüktür. İkisi de pozitif ise kökler toplamı da çarpımı da pozitiftir. İkisi de negatif ise, kökler çarpımı gene pozitiftir, kökler toplamı negatiftir. Biri negatif biri pozitif ise kökler çarpımı negatiftir, ancak toplam hakkında birşey söyleyemeyiz. Bir negatif bir pozitif sayının toplamı bu sayıların mutlak değerine bağlıdır. Yani köklerin mutlak değerleri hakkında da bir bilgi verilmesi gerekir.
\begin{align*}
0 \lt x_1 &\leq x_2 \Rightarrow -\frac{b}{a} \gt 0 \text{ ve } \frac{c}{a} \gt 0\\
x_1 \leq x_2 & \lt 0 \Rightarrow -\frac{b}{a} \lt 0 \text{ ve } \frac{c}{a} \gt 0\\
x_1 \lt 0 & \lt x_2 \Rightarrow \frac{c}{a} \lt 0 \text{ ve } -\frac{b}{a}\quad ??
\end{align*}
[note1]$x_1 \lt 0 \lt x_2$ durumunda kökler toplamı $-\frac{b}{a}$ nın değeri için üç ihtimal olduğu açıktır. Toplam, mutlak değerce büyük olanın işaretini alır, eşitlerse toplam $0$ olur.[/note]
Örnek
$2x^2-mx+m^2-1=0$ denkleminin kökleri $x_1$ ve $x_2$ dir.
\[ x_1 \lt 0 \lt x_2 \text{ ve } |x_1| \lt |x_2| \] olduğuna göre $m$ nin alabileceği değerlerin aralığı nedir?
Çözüm
Kökler ters işaretli, dolayısıyla $x_1\cdot x_2 = \frac{c}{a} \lt 0$. Negatif olanın mutlak değeri daha küçük, demek ki toplamları pozitif, $x_1 + x_2 = -\frac{b}{a} \gt 0$.
\[ \frac{c}{a} = \frac{m^2-1}{2} \lt 0 \Rightarrow m^2 - 1 \lt 0 \]
$m^2 -1 \lt 0$ eşitsizliğini gerçekleyen $m$ ler $(-1,1)$ aralığındadır.
\[ \frac{-b}{a} = \frac{m}{2} \gt 0 \Rightarrow m \gt 0 \]
İki çözümü kesiştirdiğimizde \[ 0 \lt m \lt 1 \text{ ya da } m\in (0,1) \]
Son olarak çözüm kümesinin $\Delta \geq 0$ eşitsizliğine uyup uymadığına bakmalıyız. Daha önce belirtildiği gibi söylenmese de kökler reel olmak zorundadır.
\begin{align*}
b^2 - 4ac = m^2 - 8 (m^2 -1 ) & \gt 0 \\
-7m^2 + 8 & \gt 0 \\
m^2 & \lt \frac{8}{7}
\end{align*}
Çözüm kümesi, eşitsizliğe uymaktadır.
Örnek
$mx^2 - 3x + 1=0$ denkleminin köklerinin pozitif olması için $m$ hangi aralıkta olmalıdır?
Çözüm
Kökler pozitif ise hem çarpım hem de toplamları pozitiftir.
\[ \frac{-b}{a} = \frac{3}{m} \gt 0 \Rightarrow m \gt 0 \]
\[ \frac{c}{a} = \frac{1}{m} \gt 0 \Rightarrow m \gt 0 \]
Ancak $m$ değerleri, $\Delta \geq 0$ eşitsizliğini de sağlamalı.
\begin{align*}
\Delta=b^2-4ac=9-4m^2 &\geq 0 \\
9 &\geq 4m^2\\
\frac{9}{4} &\geq m^2 \Rightarrow \\
-\frac{3}{2} &\leq m \leq \frac{3}{2}
\end{align*}
İki eşitsizliğin kesişim kümesi \[ m \in (0,\frac{3}{2}] \]
* $k\neq 0$
Burada da gene $k$ nın kökler arasında olduğu durumu ayrı, köklerin dışında olduğu iki durumu da ayrı inceleyelim. Önce $k$ nın arada olduğu duruma grafikle bakalım.
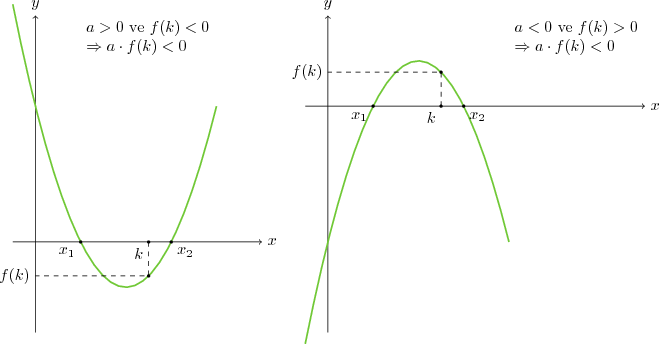
Grafikten de görüldüğü gibi
* $a\cdot f(k) \lt 0$ ise $x_1 \lt k \lt x_2$ dir.
Şimdi de $k$ sayısının köklerin ikisinden de küçük ya da büyük olduğu duruma bakalım.
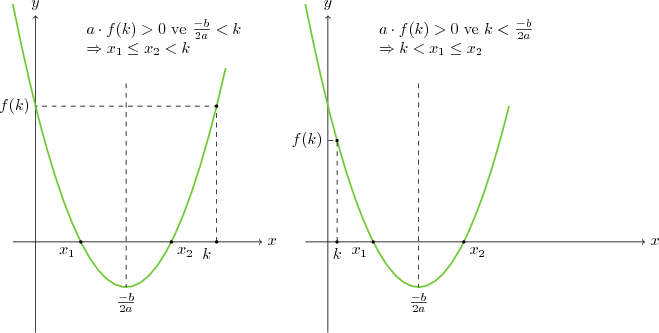
* $a\cdot f(k) \gt 0$ ise $k$ köklerin dışındadır.
\[ k \lt x_1 \leq x_2 \qquad x_1 \leq x_2 \lt k\] durumlarından hangisinin geçerli olduğunu belirlemek için $\frac{-b}{2a}$ ya bakılır. [note2]Buradaki mantık $a\cdot f(k) \gt 0$ ise $k$ ya iki kökten de küçüktür ya da iki kökten de büyüktür. Köklerin tam ortasından, yani $\frac{-b}{2a}$ dan küçükse, en az bir kökten küçüktür, dolayısıyla ikisinden de küçüktür[/note]
$k$ nın kökler dışındaki durumunu, sadece kolları yukarı olan bir parabolde ($a \gt 0$) inceledik. Kollar aşağı doğruyken hem $a$ hem de $f(k)$ nın negatifliği açıktır. Dolayısıyla çıkarımlar aynıdır.
Örnek
$ x^2 - ax -3=0$ denkleminin kökleri $x_1$ ve $x_2$ dir. $ x_1 \lt 1 \lt x_2 $
şartını sağlayan en küçük $a$ tam sayısı nedir?
Çözüm
$k=1$ sayısının köklerin arasında olması isteniyor. Burada sadece $a\cdot
f(k) \lt 0$ şartı sağlanmalı. \[ f(1) = 1-a-3 = -a-2 \lt 0 \Rightarrow a \gt -2 \]
En küçük $a$ tam sayısı $-1$ dir.
Örnek
$ -mx^2 - (m-2)x + 4 =0$ denkleminin kökleri $x_1$ ve $x_2$ dir. \[ x_1 \lt -1
\lt x_2 \] şartını sağlayan en küçük $m$ tam sayısı nedir?
Çözüm
Gene kökler arasında olması istendiğinden $a\cdot f(k) \lt 0$ şartı sağlanmalı.
Burada $a = - m $ ve $k=-1$ dir.
\[ a \cdot f(k) = -m \cdot (-m+m-2 + 4)=-2m \lt 0 \Rightarrow m \gt 0 \]
En küçük $m$ tam sayısı $1$ dir.
Örnek
$x^2 - 6x + 6=0$ denkleminin kökleri ile $1$ arasındaki ilişkiyi belirleyiniz.
Çözüm
Önce $a \cdot f(k)$ değerine bakalım.
\[ a \cdot f(k) = 1^2 - 6 + 6 =1 \gt 0 \] $a \cdot f(k)$ pozitif olduğundan $1$ köklerin dışındadır. $k$ sayısı $\frac{-b}{2a}=3$ değerinden küçük olduğundan iki kökten de küçüktür.
\[ 1 \lt \frac{-b}{2a} \Rightarrow 1 \lt x_1 \leq x_2 \]
