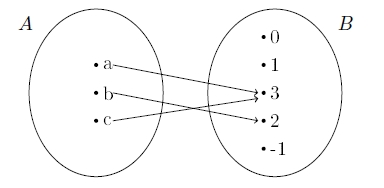
$A=\{ a,b,c \}$ fonksiyonun tanım kümesidir.
$B=\{ 3,2,1,0,-1 \} $ fonksiyonun değer kümesidir.
$a \in A $'nın $f$ altındaki görüntüsü (değeri) $f(a)=3$
$b \in A $'nın $f$ altındaki görüntüsü (değeri) $f(b)=2$
$c \in A $'nın $f$ altındaki görüntüsü (değeri) $f(c)=3$'tür.
$A$'nın $f$ altındaki görüntü kümesi
$f(A)=\{ 2,3 \} $'dir.
$f$ bağıntısı $f= \{ (a,3), (b,2), (c,3) \} $'dir.

$ \forall \: x \in \mathbb{R} $ için $ y=3x-4 \in \mathbb{R} $ olduğundan $f \;$ bağıntısı bir fonksiyondur.

Bir bağıntının fonksiyon olabilmesi için bir elemanın sadece bir görüntüsü olması gerekir. $x$ yerine örneğin $0$ verdiğimizde $ |y|=1$ olur. Buradan da $y=1$ ve $y=-1$ değerleri çıkar, tanım kümesinden bir eleman değer kümesinden iki elemanla eşleşmek zorunda kalır.

$f(-3)= \frac {2} {5} , \; f(-2)= \frac {1} {4} , \; f(-1)=0 , \; f(0)= - \frac {1} {2} , \; f(1)=-2 $

$f(A)= \{ \frac {2} {5}, \frac {1} {4}, 0, - \frac {1} {2}, -2 \} $


$f= \{ (-3, \frac {2} {5}), ( -2, \frac {1} {4}) , (-1, 0 ) , (0, - \frac {1} {2}), ( 1, -2) \} $

$f(6)= f(4+2)=4 \, f(4) -3 = 4 \cdot 5 -3=17 $
$f(8)= f(6+2)=6 \, f(6) -3 = 6 \cdot 17 -3=99 $

$f(x)=4+f(x-1) \Rightarrow f(x)-f(x-1)=4 $
$x=2 \Rightarrow f(2)-f(1)=4$
$x=3 \Rightarrow f(3)-f(2)=4$
$x=4 \Rightarrow f(4)-f(3)=4$
$ \vdots $
$x=15 \Rightarrow f(15)-f(14)=4$
$f(15)-f(1)=14 \cdot 4=56$
$f(15)=56+3=59$

$3x-4=5 \Rightarrow x=3 \Rightarrow f(5)= \sqrt {3^3-5}+3= \sqrt{16}+3=7$

$2x+2=6 \Rightarrow x=2 , \quad f(2\cdot 2+2)= f(6)=2^3-2\cdot 2=4$
$2x+2=-4 \Rightarrow x=-3 \quad f(2\cdot (-3)+2)= f(-4)=3\cdot(-3)+4=-5$
f(6)+f(-4)=4+(-5)=-1$

\begin{align*}
f(-3,-2) &= min((-3)^2-1, \; (-3)\cdot (-2)+1) \\
&= min(8, \, 7)=7 \\
& \\
g(3,2) &= max(3+2\cdot 2+1, \; 2\cdot 2-2) \\
&= max(8, \, 2) =8 \\
\end{align*}
$2f(-3,-2)+g(3,2)=2\cdot 7+8=22$

$f(x)$ fonksiyonu birebir değildir çünkü görüntü kümesindeki her bir eleman tanım kümesindeki tek bir $x$ ile eşleşmez.
Örneğin $x$ yerine $2$ veya $-2$ , $f(2)=5 \quad $ $ f(-2)=5 $ , koyduğumuzda fonksiyondan çıkan sonuç $5$ olur, tanım kümemizdeki iki değerin de değer kümesindeki görüntüsü aynıdır, bu yüzden birebir değildir.

$f(x)$ fonksiyonu sabit bir fonksiyondur, yani tanım kümesindeki tüm elemanların değer kümesinde eşleştiği tek bir eleman olmalıdır. Bu durumda $x$ yerine ne koyarsak koyalım çıkan sonucun değişmemesi lazım olduğuna göre $x$'li tüm ifadelerin katsayısı $0$ olmalıdır. $x$'li ifadelerin katsayıları
\begin{align*}
4a+4&=0 \\
a &=-1 \\
& \\
b-3 &=0 \\
b &=3 \\
\end{align*}
sonucuna ulaşırız.
\begin{align*}
f(x)&=0 \cdot x^2+ 0 \cdot x+3\cdot (-1)-2\cdot 3 \\
f(x)&= -9 \\
\end{align*}
Bu durumda $x$ yerine ne koyarsak koyalım alacağımız sonuç aynı olur ve $f(5)=-9$'dur.

$f(x)$ fonksiyonunun birim (özdeş)fonksiyon olması için $f(x)=x$ olmalıdır, bu durumda
\begin{align*}
3a+8&=1\\
a &= - \frac {7} {3}\\
& \\
2a-3b&=0 \\
2\cdot ( -\frac {7}{3} )-3b &=0 \\
b &= - \frac {14}{9} \\
& \\
a\cdot b&= (- \frac {7} {3} ) \cdot (- \frac {14}{9} ) \\
a\cdot b&= \frac {98}{27} \\
\end{align*}
sonucuna ulaşırız.

Bir fonksiyonunun doğrusal olması için, fonksiyonun kartezyen düzlemdeki grafiğinin bir doğru oluşturması gerekir. Bunun için fonksiyon $f(x)=ax+b$ şeklinde olmalıdır.
\begin{align*}
f(3)=8 &\rightarrow 3a+b=8 \\
f(-2)=-7 &\rightarrow -2a+b=-7 \\
\text {üstteki ifadeden alttaki ifadeyi çıkarırsak,} \\
5a&=15 \Rightarrow a=3 \\
3\cdot 3+b &=8 \\
b&=-1 \\
\end{align*}
sonucuna ulaşırız.
$f(x)=3x-1$
ve
$f(5)=14$

$f(x)$ doğrusal ise $f(x)=ax+b$ şeklinde olmalıdır.
\begin{align*}
f(x+3)&=a(x+3)+b \quad & f(4x+5)&=a(4x+5)+b \\
&=ax+3a+b \quad & &=4ax+5a+b\\
& \\
\end{align*}
\begin{align*}
f(x+3)+f(4x+5) &=10x \\
ax+3a+b+4ax+5a+b &=10x \\
5ax+8a+2b&=10x \\
\end{align*}

\begin{align*}
5ax &=10x \quad & 8a+2b&=0 \\
a &=2 \quad & 8\cdot 2+2b&=0 \\
& \quad & b&=-8 \\
\end{align*}
sonucuna ulaşırız. Böylece
$f(x)=2x-8$ olur.

$f(x)=3x^2-3$ olduğuna göre,
\begin{align*}
f(-x)&=3(-x)^2-3 \\
&=3x^2-3 \\
&=f(x) \\
\end{align*}

$f(-x)=f(x)$ olduğundan $f$ çift fonksiyondur.

$f(x)=5x^3-x$ olduğuna göre,
\begin{align*}
f(-x)&=5(-x)^3-(-x) \\
&=-5x^3+x \\
&=-f(x) \\
\end{align*}

$f(-x)=-f(x)$ olduğundan $f$ tek fonksiyondur.
Bir fonksiyonun tek fonksiyon olması demek çift dereceli terimlerin katsayıları sıfır olmalıdır, çift olması için de tek dereceli terimlerin katsayıları sıfır olmalıdır.

$f(x)=(4a+8)x^3+(2b-2)x^2+(3b-6)x+a-2b$ çift olması için sadece çift dereceli terimlerden oluşması gerekir.
Yani tek dereceli terimlerin katsayıları $0$ olmalıdır.
\begin{align*}
4a+8&=0 & 3b-6&=0 \\
a&=-2 & b&=2 \\
\end{align*}
\begin{align*}
f(x) &=0\cdot x^3+2x^2+0 \cdot x-6 \\
f(x) &=2x^2-6 \\
\end{align*}
\begin{align*}
f(2) &=2\cdot 2^2-6 \\
&=2 \\
\end{align*}

$f+g$ toplam fonksiyonu $A\cap B= \{ 0,1,4 \} $ kümesinde tanımlıdır. Bu yüzden $0$, $1$ ve $4$'ün görüntülerini bulmalıyız.

\begin{align*}
(f+g)(0) &= f(0)+g(0) \\
&=0+2+0-5 \\
&=-3 \\
\end{align*}

\begin{align*}
(f+g)(1) &= f(1)+g(1) \\
&=1+2+1-5 \\
&=-1 \\
\end{align*}

\begin{align*}
(f+g)(4) &= f(4)+g(4) \\
&=4+2+16-5 \\
&=17 \\
\end{align*}


Bu durumda $ f+g$ toplam fonksiyonunun görüntü kümesi
$ \{-3,-1,17 \} $ olur.

\begin{align*}
g(x)&=3x+2 & g(2)&=3\cdot 2+2 \\
& & &=8\\
\end{align*}

\begin{align*}
f(x) &= x^3+3 & f(2)&=2^3+3 \\
& & &=11 \\
\end{align*}

\begin{align*}
(2g+f\cdot g-3)(2)&=2g(2)+f(2)\cdot g(2)-3 \\
&=2\cdot 8+11\cdot 8-3 \\
&=101
\end{align*}

\begin{align*}
f&= \{ (1,-2), (2,3), (4,0),(8,5) \} \\
f(2)&=3 \qquad \qquad \qquad \qquad \qquad \text{ ise } & f^{-1}(3)&=2 \\
f(4)&=0 \\
f(8)&=5 \qquad \qquad \qquad \qquad \qquad \text{ ise } & f^{-1}(5)&=8 \\
\end{align*}
Bu durumda
\begin{align*}
f^{-1}(3)+f(4)-f^{-1}(5)&=2+0-8 \\
&=-6 \\
\end{align*}

\begin{align*}
2x+3&=1 \qquad \qquad \qquad \qquad \qquad \rightarrow & x&=-1 \\
x&=-1 \qquad \qquad \qquad \qquad \qquad \rightarrow & f(-1)&=3 \cdot (-1)-4=-7 \\
\end{align*}
\begin{align*}
f(2x+3)&=3x-4 \rightarrow & f^{-1}(3x-4)&=2x+3 \\
& & 3x-4&=5 \rightarrow x=3 \\
x&=3 & \rightarrow f^{-1}(5)&=2\cdot 3+3=9 \\
\end{align*}
Bu durumda
\begin{align*}
f(1)+f^{-1}(5)&=-7+9 \\
&=2\\
\end{align*}