Ters Trigonometrik Fonksiyonların Türevi
| $\arcsin u $ | $\arccos u $ | $\arctan u $ | $\DeclareMathOperator{\arccot}{arccot} \arccot u $ |
|---|---|---|---|
| $\displaystyle\frac{u'}{ \sqrt{1-u^2}} $ | $- \displaystyle\frac{u'}{ \sqrt{1-u^2}} $ | $\displaystyle\frac{u'}{ 1+u^2 } $ | $ - \displaystyle\frac{u'}{ 1+u^2 } $ |
Çözümlü Örnekler I
Örnek
$ y = \arcsin(x^2)$ ise $\frac{dy}{dx} $ nedir?Çözüm
$y' = \frac{2x}{\sqrt{1-x^4}} $Örnek
$y = \arcsin(\sqrt{x})$ ise $\frac{dy}{dx}$ nedir?Çözüm
\[ y ' = \frac{\frac{1}{2\sqrt{x}}}{\sqrt{1 - x}} = \frac{1}{2\sqrt{x-x^2}} \]Örnek
$ y = \arcsin(3^x) $ ise $ \frac{dy}{dx} $ nedir?Çözüm
$ \frac{3^x \cdot \ln 3}{1 - 9^x} $Örnek
$ y = \arcsin(\ln x)$ ise $\frac{dy}{dx} $ nedir?Çözüm
\[ \frac{1}{x \sqrt{1 - \ln^2 x}} \]Örnek
$y = \arccos(\frac{x}{4})$ ise $\frac{dy}{dx}$ nedir?Çözüm
\[ -\frac{ \frac{1}{4}}{\sqrt{1-(\frac{x}{4})^2}} = -\frac{1}{16 \sqrt{16 - x^2}} \]Örnek
$y = \arctan(\sin x)$ ise $\frac{dy}{dx}$ nedir?Çözüm
\[ y' = \frac{ \cos x}{1 + \sin^2 x} \]Örnek
$y = \arctan(\tan x)$ ise $\frac{dy}{dx}$ nedir?Çözüm
$ \arctan $ ve $\tan $ birbirinin tersi olduğundan $\arctan(\tan x) = x$ tir. $y'= 1 $
Örnek
$y = \ln(\arctan x)$ ise $\frac{dy}{dx}$ nedir?Çözüm
\[ \frac{(\arctan x)'}{\arctan x} = \frac{1}{\sqrt{1+x^2} \arctan x} \]
Ters Fonksiyonun Türevi
Bir $f$ fonksiyonu için $f(x_0) = y_0$ olsun. $f$ in tersi $f^{-1}$ bir fonksiyonsa, $f$ fonksiyonu $x_0$ noktasında türevlenebilir ise ve $f'(x_0) \neq 0 $ ise $ [f^{-1}]'(y_0) $ vardır ve şuna eşittir:
\[ [f^{-1}]'(y_0) = \frac{1}{f'(x_0)} \]
Bu formül bir fonksiyonun tersini almadan tersinin türevinin belli bir değerini bulmamıza yarayacak. Örneklerde uygulamaları görülecektir.
Çözümlü Örnekler II
Örnek
$ f:[0, + \infty) \to [-1, + \infty)$ ve $f(x) = x^2 -1 $ ise $[f^{-1}]'(3) = ? $
Çözüm
Önce fonksiyonun türevini alalım: $ f'(x) = 2x$.
$y_0 = 3$ verilmiş. Fonksiyonda bu görüntüyü veren $x$ i bulmalıyız: $ x^2 -1 = 3 \to x = \pm 2$. Tanım kümesi gereği $x = 2$ dir.
Şimdi formülü uygulayalım:
\[ [f^{-1}]'(y_0) = \frac{1}{f'(x_0)} \Rightarrow [f^{-1}]'(3) = \frac{1}{f'(2)} = \frac{1}{2 \cdot 2} = \frac{1}{4} \]
II. Yol
Eğer kolayca bulunabiliyorsa fonksiyonun tersini bulabiliriz. Bu durumda zaten tersin türevini alıp istediğimiz değeri koyarız. Ancak tersin türevi ile ilgili soru sorulmuşsa büyük olasılıkla yukarıdaki formülle çözülebilecek ve tersini almanın zor olduğu bir fonksiyon verilecektir. Örneğin bir sonraki örnekte ters almak çok mümkün değil.
\[ y = x^2 -1 \to y + 1 = x^2 \to \pm\sqrt{y+1} = x \to f^{-1} x = \sqrt{y+1} \]
Son adımda $-\sqrt{x+1}$ ya da $+ \sqrt{x+1}$ e fonksiyonun tanım kümesine bakarak karar verilir. Burada tanım kümesi $[0, + \infty)$ olduğundan tersin görüntü kümesi yani ters fonksiyonda çıkacak değerler bu küme içindedir.
Artık tersin türevini bulabiliriz. \[ \frac{1}{2 \sqrt{x+1}} \to [f^{-1}]'(3) = \frac{1}{2 \sqrt{3+1}} = \frac{1}{4} \]
Ters fonksiyon bulunuşu için buraya bakılabilir.
Örnek
$f(x) = x^3 + x $ ise $ [f^{-1}]'(2) = ? $
Çözüm
Önce türev alalım: $f'(x) = 3x^2 +1$. Fonksiyonun $2$ yapan $x$ değerini bulalım: $x^3 + x = 2 \to x =1$
Formülü uygularsak:
\[ [f^{-1}]'(y_0) = \frac{1}{f'(x_0)} \Rightarrow [f^{-1}]'(2) = \frac{1}{f'(1)} = \frac{1}{3 \cdot 1^2 + 1} = \frac{1}{4} \]
Kapalı Fonksiyonun Türevi
Kapalı fonksiyonlarda $y$ ya da $f(x) $ in $x$ e bağlı ifadesi direk verilmemiştir. Bunu elde etmek zor veya imkansız olabilir. Bu durumda buradaki formülleri kullanacağız.
Kapalı fonksiyon $ F(x,y) = 0$ şeklindeki fonksiyondur. Yani $x$ ve $y$ nin karışık bir ifadesi sıfıra eşittir. Burada kapalı ile anlatılmak istenen $y$ nin $x$ cinsinden eşitinin açık olmamasıdır.
Alışıldık bir örnek olarak birim çember denklemini verebiliriz. Birim çembere $x = \frac{1}{2}$ noktasından çizilen ve ordinatı pozitif olan teğetin eğimini, dolayısıyla $f'(\frac{1}{2})$ değerini bulmaya çalışalım.
Birim çemberin denklemi \[ x^2 + y^2 =1 \]
Birim çember denklemini açık bir fonksiyon olarak yazmak istersek $y^2 = 1-x^2 \to y = \pm \sqrt{1-x^2} $
Grafikte de görüldüğü gibi üst kısım $y = +\sqrt{1-x^2}$ ve alt kısım da $ y = -\sqrt{1-x^2}$ dir.
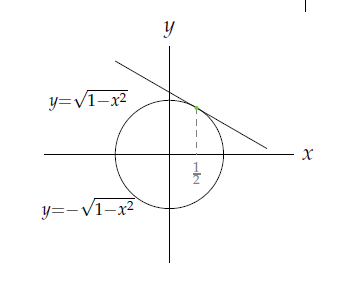
Üst kısmın türevi \[ y' = \frac{-x}{\sqrt{1-x^2}} \]
Teğet eğimi $y'(\frac{1}{2}) = - \frac{1}{\sqrt{3}} $
$y = f(x) $ olduğundan verilen kapalı fonksiyon $x^2 + f^2(x) = 1$ şeklinde de yazılabilir. Buraya kadar ki türev alma bilgimizle bu eşitliğin iki yanının türevini alalım:
\[( x^2 + f^2(x) )' = 1' \to 2x + 2 f(x) + f'(x) = 0\]
Bulmak istediğimiz değer $f'( \frac{1}{2})$ olduğundan $x = \frac{1}{2}$ koyarsak $ 1 + 2 f(\frac{1}{2}) f'(\frac{1}{2}) = 0 $.
$ f(\frac{1}{2})$ değeri için fonksiyonu kullanırsak \[ x^2 + y^2 = 1 \to \frac{1}{4} + y^2(\frac{1}{4}) = 1 \to y(\frac{1}{4})= \pm \frac{\sqrt{3}}{2} \]
Ordinatı pozitif olan teğet için $ y(\frac{1}{2}) = \frac{\sqrt{3}}{2} $ olur. Bunları türev içeren ifadede koyarsak:
\[ 1 + 2 f(\frac{1}{2}) f'(\frac{1}{2}) = 0 \to f'(\frac{1}{2}) = - \frac{1}{\sqrt{3}} \]
Fonksiyonu yani $y$ yi $x$ cinsinden çekemeyeceğimiz kapalı fonksiyonlar da var. Şöyle bir fonksiyon düşünelim: \[ x^2 - 5y^2x - xy = 0\]
Burada $y$ yi çekmekden $f(2)$ yi bulabiliriz. $x$ yerine $2$ yazıp $y$ yi çekeriz. Ancak $y$ yi $x$ cinsinden çekemeyiz.
Bu tip fonksiyonlarda $\frac{dy}{dx}$, yani $y$ nin $x$ e göre türevini bulmak için pratik bir kural uygulanır. Bu kuralı vermeden önce şu ana kadar öğrendiklerimizle bulmaya çalışalım. Öncelikle $y$ nin $x$ in bir fonksiyonu olduğunu hatırlayalım, yani $y = f(x) $ tir ve $y' = f'(x)$ tir. Ancak $x$ bağımsız değişkendir ve türevi $1$ dir.
Örneğin $x \cdot f(x)$ ifadesinin türevi $ \left( x f(x) \right)' = 1 \cdot f(x) + x \cdot f'(x)$ tir. Bunu şöyle de yazabiliriz: $ (xy)' = y + xy' $. Bir çarpma var ve çarpma kuralı uyguladık. Örneğin $y^2$ nin türevi $2yy'$ olur. Bunu zaten biliyoruz ancak böyle yazınca kafa karışıklığı yaratıyor. $f^2(x) $ in türevi $2 f(x) f'(x)$ tir.
Dolayısıyla yukarıdaki fonksiyonun türevi şöyle alınır:
\begin{align*}
(x^2 - 5y^2x - xy)' &= (x^3 y)' - (5y^2 x)' - (xy)' = 0\\
&= (2x )- (10y y' x + 5y^2) - (y + xy') = 0 \\
\end{align*}
Türevi saf olarak elde edemesek de istediğimiz değerini bulabiliriz. Örneğin verilen fonksiyona $x =4$ apsisli noktasından çizilen teğetin eğimini bulalım. $y'(4)$ için $x = 4 $ yapacağız. $ y = f(x)$ ve $y' = f'(x)$ olduğunu unutmayalım.
\begin{align*}
(2x)- (10y y' x + 5y^2) - (y + xy') &=0 \\
(8) - (10 y(4) y'(4)+ 5 y^2(4)) - (y(4) + 4 y'(4)) &= 0
\end{align*}
$y(4)$ değeri için verilen fonksiyonu kullanacağız: \[ x^2 - 5y^2x - xy = 0 \to 16 - 20y^2(4) - 4 y = 0 \to 5y^2 + y -16 = 0 \]
Son denklem çarpanlara ayrılıp çözülürse $ y = \frac{4}{5}$ ve $y = -1$ çıkar. Demek ki apsisi $4$ olan iki teğet var. Biz $y = \frac{4}{5} $ in eğimini bulmaya çalışalım.
Bu değeri bulduğumuz türev ifadesinde yerine yazarsak:
\begin{align*}
(2x )- (10y y' x + 5y^2) - (y + xy') &= 0 \\
8 - 32y' - \frac{16}{5} -\frac{4}{5} - 4y' &= 0 \\
y' &= \frac{1}{9}
\end{align*}
Yukarıdaki yolun özetlenmiş hali olarak şöyle bir kural uyguluyoruz.
$ F_x $ verilen fonksiyonun $x$ değişken $y$ sabit sayı olarak düşünülen türevi ve $F_y $ fonksiyonun $y$ değişken $x$ sabit sayı olarak düşünülen türevi olmak üzere verilen $F(x,y)$ fonksiyonunun türevi $\frac{dy}{dx}$ şuna eşittir:
\[ \frac{dy}{dx} = - \frac{F_x}{F_y} \]
Örneğin yukarıda incelediğimiz fonksiyon $ x^2 - 5y^2x - xy =0$ için bunu uygulayalım:
\[ F_x = 2x - 5y^2 - x \]
$y$ yi bir sayı olarak düşündüğümüzden türeve hiçbir etkisi yoktur, aynen $5$ nasıl dışarı çıkıyorsa $y^2$ de dışarı çıkar( $5y^2 x $ nin türevi $5y^2$ oldu).
\[ F_y = -10xy - x \]
\[ \frac{dy}{dx} = - \frac{F_x}{F_y} = - \frac{2x- 5y^2 - x}{-10xy - x} \]
$x = 4$ noktasındaki teğetlerin eğimleri için bu değeri yerine yazarsak
\[ y'(4) = - \frac{8 - 5y(4)^2 - x}{-80y(4) - 4}\]
$y(4)$ değerini yukarıdaki incelemede yapıldığı gibi gene ilk fonksiyona gidip bulmalıyız.
