• ders
• video
• test

Fonksiyon Tanımı

* İlk kümedeki her eleman ikinci kümedeki bir elemanla eşleşecek
* İlk kümenin hiç bir elemanı ikinci kümede birden fazla elemanla eşleşmeyecek.

Bildiğimiz gibi kartezyen çarpım bir kümenin elemanları ile başka bir kümenin elemanlarının eşleştirilmesiyle ortaya çıkan küme idi.
$ A=\{1,2,3\}\quad B=\{a,b\} $ olsun. Bu durumda
\[A\times B=\{(1,a),(1,b),(2,a),(2,b),(3,a)\}\]
İkililerden oluşan bu kümenin herhangi bir alt kümesi bir bağıntı idi. Yukarıdaki kartezyen çarpımdan bir kaç bağıntı yazalım:

1. $\beta_{1} = \{(1,a)(2,b)\} $


2. $\beta_{2} = \{(1,a),(2,a),(3,a)\}$


3. $\beta_{3} = \{(1,a),(1,b),(2,a),(3,b)\}$

1. $\beta_{1}$ bir fonksiyon değildir, çünkü $A$ kümesinin bir elemanı olan $3$, $B$ de bir elemanla eşlemiyor.

   
   



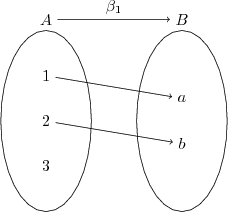
2. $\beta_{2}$ bir fonksiyondur çünkü $A$'nın bütün elemanları $B$'de bir elemanla eşleşiyor. $A$'nın bütün elemanlarını $B$'nin aynı elemanına eşleştirmekte ve $B$'de boşta eleman kalmasında bir sakınca yok.

   
   



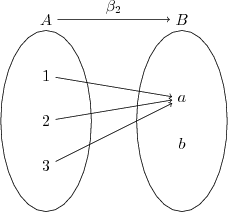
3. $\beta_{3}$ bir fonksiyon değildir, çünkü $1$ $B$'nin iki elemanıyla eşleştirilmiş.

   
   

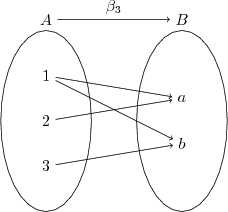
Bir $A$ kümesinden $B$ kümesine yazılabilecek fonksiyon sayısı, bu durumda bağıntı sayısına eşit değil, $s(B)^{s(A)}$ olmaktadır. Çünkü $A$ dan alınan herhangi bir elemanı $B$ de tek bir elemana eşleyeceğiz ve $s(B)$ tane seçeneğimiz var. Daha somut bir örnekle, elimizde $3$ mektup ve $4$ posta kutusu olsun. Mektupları mutlaka postalayacağız, ve istediğimiz posta kutusuna atabiliriz. Bu durumda kaç değişik eşleştirme yapabiliriz? [note1]Bütün mektuplar postalanacak kuralı tanım kümesinde boşta eleman kalmama şartını, bir mektubun iki ayrı posta kutusunda olamaması da, bir elemanın iki farklı görüntüsü olmama şartını sağlıyor.[/note]
Her bir mektup için $4$ ayrı seçeneğimiz olduğundan $4^3$ değişik seçim yapılabilir.

Genellikle sayı kümelerinden sayı kümelerine eşleştirme yapan fonksiyonlarla ilgileneceğiz. Bu fonksiyonlarda da birinci kümeden alınan bir elemanın ikinci kümede hangi elemana eşleştirildiğini veren bir kural olacak.

Önce bir kaç tanım yapalım:
Eşleştirme yapılan birinci kümeye anım kümesi, ikinci kümeye de değer kümesi denir. Fonksiyonlar genellikle $f,g,h$ gibi harflerle gösterilir ve eşleştirmenin hangi kümeden hangi kümeye yapıldığını belirtmek için ok işareti, $\rightarrow$ kullanılır. Tanım kümesinden alınan bir $a$ elemanı, değer kümesindeki bir $b$ elemanına eşleştiriliyorsa $b$ ye $a$ nın görüntüsü denir.

$f:\mathbb{N}\rightarrow\mathbb{N}$ ifadesinde $f$ doğal sayılar kümesinden doğal sayılar kümesine eşleştirme yapıyor demektir.
Örneğin $f:\mathbb{N}\rightarrow\mathbb{N}$ ve $f(x)=x+3$ fonksiyonu doğal sayılar kümesinin her elemanını üç fazlası ile eşleştiriyordur.

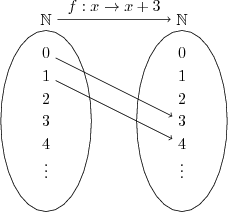
Dikkat edersek değer kümesindeki üç eleman boşta kalıyor. $\{0,1,2\}$ elemanlarına tanım kümesinden bir eleman eşlenmiyor, bu elemanların görüntüleri yok. Tanım kümesindeki elemanların değer kümesindeki karşılıklarının yani görüntülerinin oluşturduğu kümeye de görüntü kümesi denir. Örnekten de anladığımız gibi görüntü kümesi değer kümesinin bir altkümesidir, bunların her zaman eşit olması gerekmez. Yani fonksiyon değer kümesinin tamamını kullanmak zorunda değildir, ancak tanım kümesinin tamamını eşleştirmek zorundadır.