Bire-bir Fonksiyon
Tanım kümesindeki her elemanın değer kümesinde yalnız ve yalnız bir karşılığı varsa fonksiyon birebir 'dir. Örneğin
\[ f:\mathbb{R}\rightarrow\mathbb{R} \text{ ve } f(x)=2x-5 \]
$x$ değiştikçe iki katının beş fazlası da değişecektir. Bunu ispatlayalım. İki faklı elemanın $x_1$ ve $x_2$ nin görüntüleri eşit olsun.
\begin{align*}
x_1\neq x_2 \quad f(x_1) &= f(x_2)\\
2x_1-5 &= 2x_2-5\\
x_1 &= x_2
\end{align*}
Görüntüleri eşitleyen denklemin tek çözümü $x_1=x_2$ dir. Ancak biz $x_1 \neq x_2$ almıştık.
Tersi bir örnekle daha iyi anlaşılacaktır.
Örnek
$f:\mathbb{R}\rightarrow\mathbb{R} \text{ ve } f(x)=x^2-2$ ise fonksiyon bire-bir midir?
Çözüm
Bu durumda, örneğin, hem $f(-3)=7$ hem de $f(3)=7$ çıkar. Her sayının hem negatif hem de pozitif değeri aynı görüntüyü verir, yani fonksiyon bire-bir değildir. Önceki örnekteki gibi genel bir ispat yaparsak:
\begin{align*}
x_1\neq x_2 \quad f(x_1) &= f(x_2)\\
x_1^2 &= x_2^2 \Rightarrow\\
x_1 &= x_2 \text{ ve } x_1 = -x_2
\end{align*}
Görüntüleri eşitleyen denklemin iki çözümü var. Biri $x_1=x_2$ olmalı diyor, ancak diğeri, biri diğerinin ters işaretlisi olabilir diyor.
Bu örnekten anlaşılan bir nokta da, sadece $x$'in çift üslerini içeren fonksiyonlar eğer tanım kümesi uygunsa bire-birdir. Yukarıdaki örnekte fonksiyonu şöyle tanımlasaydık bire-bir olacaktı:
\[f:\mathbb{R^{+}}\rightarrow\mathbb{R} \text{ ve } f(x)=x^2-2\]
Çünkü şimdi negatifleri almadık. Tanım kümesindeki farklı elemanların farklı görüntüleri var.
Örten Fonksiyon
Değer kümesinde boşta eleman kalmıyorsa fonksiyon örten 'dir. Başka bir deyişle, görüntü kümesi değer kümesine eşit olan fonksiyonlar örtendir. Örneğin:
\[f:\mathbb{N}\rightarrow\mathbb{N} \mbox{ ve } f(x)=x+1\]
Fonksiyon örten değildir çünkü değer kümesinde $0$ var ve tanım kümesindeki hiçbir eleman $0$'a eşlenmiyor. Değer kümesini $\mathbb{N^{+}}$ yaparsak fonksiyon örten hale gelir.
Bir fonksiyonun hem birebir hem de örten olması ilerde anlayacağımız nedenlerle
önemlidir, bu tip fonksiyonlara birebir-örten ya da bijeksiyon denir.
İçine Fonksiyon
Değer kümesinde boşta eleman kalan fonksiyonlardır.
Bazı Özel Fonksiyonlar: Sabit, Doğrusal, Birim, Parçalı, Permütasyon
* Sabit Fonksiyon
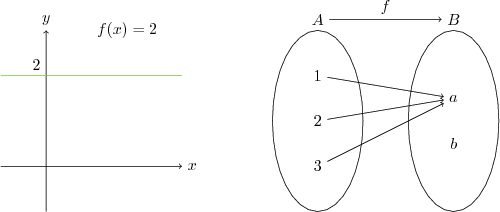
Tanım kümesindeki her elemanı değer kümesinde aynı elemana eşleyen fonksiyona sabit fonksiyon denir. Örneğin $f(x)=2$ sabit fonksiyondur ya da $f:\mathbb{N}\rightarrow \mathbb{R} \quad f(x)=\frac{3x+3}{x+1}$ sabit fonksiyondur, çünkü tüm doğal sayılar için $3$ e eşittir.
Örnek
$f(x)=(m+1)x-2$ fonksiyonu sabit fonksiyon ise $m$ ve $f(4)$ nedir?
Çözüm
Sabit fonksiyonda $x$ değişince görüntü değişmemeli. Bu da ancak $x$'i yokedersek olur. Yani $(m+1)=0$'dır. $m=-1$ ve $f(x)=-2$ olduğundan $f(4)=-2$ dir.
Örnek
$f(x)=\displaystyle\frac{2x+1}{x-a}$ sabit fonksiyon ise $a$ nedir?
Çözüm
$\displaystyle\frac{ax+b}{cx+d}$ türü fonksiyonların sabit olabilmesi için pay ve payda sabit bir orana eşit olmalı. \[\frac{a}{c}=\frac{b}{d}\]
\[\frac{2}{1}=\frac{1}{-a}\Rightarrow a=\frac{-1}{2}\]
Fonksiyon bütün $x$'leri bu orana götürür. Örnekte $f(x)=2$'dir.
* Doğrusal Fonksiyon
$f(x)=ax+b$ şeklindeki fonksiyonlar doğrusaldır. Grafikleri kartezyen düzlemde bir doğru oluşturur. Doğrusal fonksiyonlar, bire-birlik özelliği incelenirken bir örneğini gördüğümüz gibi, $a\neq 0$ ise bire-birdir. Doğrunun ayırıcı özelliği eğim dir. Eğim, $x$ teki $1$ br lik artışın $y$ de yarattığı değişimdir.
Örnek
$f(x)$ doğrusal bir fonksiyon ve $f(1)=4$, $f(3)=0$ veriliyor. Buna göre $f(-1)$ nedir?
Çözüm
I. Yol
$f(x)$ doğrusalsa $ax+b$ biçimindedir.
\begin{align*}
f(x) &=ax+b\Rightarrow \\
f(1) &= a+b = 4 \\
f(3) &= 3a+b=0
\end{align*}
İki denklemin ortak çözümünü yaparsak $a=-2$ ve $b=6$ çıkar. $f(x)=-2x+6$ dır. Buna göre
\[ f(-1)=2+6=8 \]
II. Yol
Bazan kısa olabilecek bu yolda $x$ teki $1$ br lik değişimin $y$ de yarattığı değişime bakılır.

$x$ te $2$ br lik artış $y$ de $4$ br azalışa neden oluyor. $x$ in $1$ br lik artışı $2$ azalışa denk gelir. Artık herhangi bir fonksiyon değerinden istenen değere gidilebilir. Örneğin $x=1$ için $y=4$ idi. $x=-1$ için $2$ br azaltmalıyız. Bu durumda $y$, $4$ br artar ve $8$ olur.
* Birim Fonksiyon
Her elemanı kendisine eşleyen fonksiyona birim fonksiyon denir. $f(x)=x$ ya da $I(x)=x$ biçiminde gösterilir.
* Parçalı Fonksiyon
Tanım kümesini parçalara ayırıp bunların her biri için farklı kurallar içeren fonksiyon parçalı bir fonksiyondur. Örneğin:
\[ f(x)= \left\{ \begin{array}{lrr}
2x+1 & \mbox{eger} & x \lt 0\\
3x-4 & \mbox{eger} & x \geq0
\end{array} \right. \]
$x \lt 0$ ise görüntüsünü bulmak için $2x+1$ i, değilse $3x-4$ ü kullanmalıyız.
* Permütasyon Fonksiyon
Bir kümeden kendisine yazılan bire-bir ve örten fonksiyonlara permüyasyon denir. Bu fonksiyonlar için özel olarak şöyle bir yazım kullanılır:
$A=\{1,2,3,4\}$ olsun
\[ f=\left(\begin{array}{cccc}
1 & 2 & 3 & 4\\
2 & 3 & 1 & 4\\
\end{array}\right) \]
Üstteki elemanlar tanım kümesini alttakiler de görüntüleri belirtiyor. Örneğin fonksiyon $1$ i $2$ ye, $2$ yi $3$ e götürmekte, benzer şekilde $f(3)=1$ ve $f(4)=4$ tür.
