Cevap

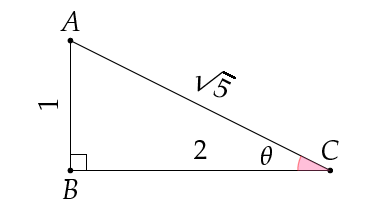$\arcsin \frac{1}{\sqrt{5}} = \theta $ olsun bu durumda $\sin \theta = \frac{1}{\sqrt{5}}$ olur. Bir diküçgen çizerek karşıya $1$ ve hipotenüse $\sqrt{5}$ verelim. Aşağıdaki üçgeni elde ederiz. $\arcsin \frac{2}{\sqrt{5}} = \beta \to \sin \beta = \frac{2}{\sqrt{5}}$ Üçgende gördüğümüz gibi $\beta$ açısı ile $BAC$ açılarının sinüsleri eşittir dolayısıyla açılar eşittir. Sorulan ifade $ \theta + \beta$ ya dolayısıyla $90$ a eşittir.