Cevap

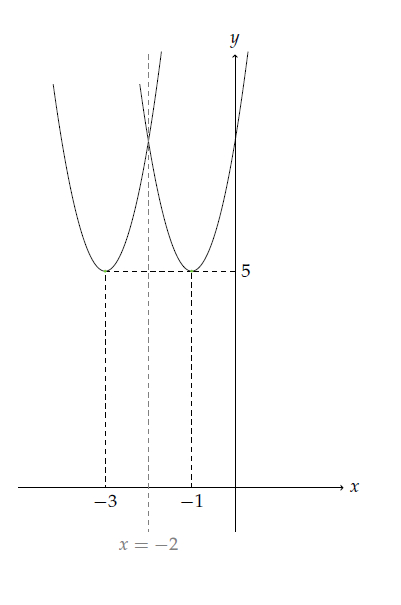1) Tepe noktası formunda verilen bir parabolün (tepe noktası $(r,k)$ olmak üzere $a(x-r)^2 + k$) $x=a$ ya göre simetriği için sadece tepe noktasını taşımamız yeterlidir. [m] y=3.(x+1)^2 +5 [/m] parabolünün tepe noktası $(-1,5)$ tir. Bu noktanın $x = -2$ doğrusuna göre simetriği çok belli ki $(-3,5)$ tir. Simetrik parabol $y=3(x+3)^2 + 5$ tir. İki parabol ve tepe noktaları şekilde görülmektedir. II. Yol. Bu yol tüm analitik geometri için geçerlidir. Herhangi bir $(x,y)$ noktasının $x=a$ doğrusuna göre simetriği $(2a-x,y)$ dir. Burada da $x=-2$ ye göre simetriği $(-4-x,y)$ dir. Yani denklemde $x$ yerine $-4-x$ koyarsak simetriği bulmuş olacağız: \[ y=3(x+1)^2 + 5 \to y = 3(-4-x+1)^2 + 5 \to 3(-x-3)^2 + 5 = 3(x+3)^2 + 5 \] 2) [m] y=x^{2}-6x+2 [/m] Herhangi bir $(x,y)$ noktasının orijine göre simetriği $(-x,-y)$ dir. Denklemde $x$ yerine $-x$ ve $y$ yerine $-y$ koymak sadece parabolde değil tüm denklemlerde orijine göre simetriği verir. $ y = x^2 - 6x + 2 \to -y = (-x)^2 - 6(-x) + 2 = x^2 + 6x + 2$. $-y = x^2 + 6x + 2 $ olduğundan $y= -x^2 - 6x -2$ 3. soru çok basit. Parabol tepe noktasından geçen dik eksene göre simetriktir. Yani $x=2$ ye göre simetrikse tepe noktasının apsisi $2$ dir. Tepe noktası apsisi $x_t= \frac{-b}{2a}$ dan $m$ değeri bulunur. 4. Soru çok temel bir soru. $x$ eksenini kesmeyen paraboller için $\Delta \lt 0$ olur. Delta ve parabol bölümünde konuyla ilgili ayrıntılı bilgi var. Lütfen tüm soruları ayrı girin ve matematik ifadeleri [m] [/m] etiketleri içine alın. Yukarıdaki soruyu da dört ayrı soru olarak girerseniz cevaplar bu soruların altına eklenecektir.