\[ A=\{ x,\{y\}, \{2,4\},5 \}\] aşağıdakilerden hangileri doğrudur?
- $x\in A$
- $\{2,4\}\in A$
- $x\subset A$
- $\{5\}\in A$
- $\{y\}\in A$
$A$ kümesinin elemanları $x$, $\{ y \} $, $\{2,4\}$ ve $5$'tir.
Buna göre 1, 2 doğru, 3 yanlıştır, $x$ bir elemandır, eğer $x$ elemanıyla şöyle bir küme oluşturulsaydı $\{ x \} $ bu küme $A$'nın altkümesi diyebilirdik ve $\{ x \} \subset A$ olarak gösterebilirdik.
4 de yanlıştır, $\{5\}$ $A$'nın bir elemanı değildir, bir altkümesidir. 5 doğrudur, $ \{y\}\ $ $A$'nın bir elemanıdır.
\[ A=\{ x,\{y,z\}, a, \{b\},c \}\] aşağılardan hangisi A kümesinin bir alt kümesi değildir?
- $\{x\}$
- $\{\{b\}\}$
- $\{y,z\}$
- $\{c\}$
- $\{a\}$
Doğru cevap $c$'dir, $\{y,z\}$ $A$'nın altkümesi değildir, doğru gösterim $\{\{y,z\}\}$ şeklinde olmalıydı.
\[ A=\{ 1,\{a,b\}, b, \emptyset \}\] şıklardan hangisi doğrudur?
- $\{b\}\in A$
- $\{\emptyset,b\} \subset A$
- $\{a,b\}\subset A$
- $\{1,a\}\subset A$
- $s(A)=5$
$A$ kümesinin elemanları $1$, $\{a,b\}$, $b$ ve $\emptyset $'dir.
Buna göre $a$ şıkkı yanlıştır, $b \in A$ şeklinde gösterseydik doğru olurdu. $b$ şıkkındaki $\{\emptyset,b\} \subset A$ ifadesi doğrudur, $ \emptyset$ ve $b$ elemanlarından oluşan bu küme $A$'nın iki elemanlı bir altkümesidir. $d$ şıkkındaki $a$ elemanı $A$ kümesinin bir elemanı değildir, $\{1,a\}\subset A$ ifadesi doğru değildir.
$A$'nın eleman sayısı $4$'tür $e$ şıkkı da yanlıştır.
\[ A=\{ \{ a \},b, \{ \emptyset \} \}\] şıklardan kaçı yanlıştır?
- $\emptyset \subset A$
- $\emptyset \in A $
- $\{b\} \subset A$
- $\{a\} \subset A$
- $\{\emptyset\} \subset A$
$A$ kümesinin elemanları $ \{ a \}$, $b$ ve $ \{ \emptyset \} $'dir.
1. ifade kümelerin tanımı gereği doğrudur, $ \emptyset $ her zaman bir kümenin altkümesidir.
2. ifade yanlıştır, $ \emptyset $ $A$'nın bir elemanı değildir, $ \{ \emptyset \} $ $A$'nın bir elemanıdır.
3. ifade doğrudur, $\{b\} $ kümesi $A$'nın da bir elemanı olan $b$ elemanından oluşan tek elemanlı bir kümedir.
4. ifade yanlıştır, $ \{ \{a\} \} \subset A$ şeklindeki bir gösterim doğru olurdu.
5. ifade de yanlıştır, $\emptyset$ $A$'nın bir elemanı olmadığı için bu küme bir altküme değildir.
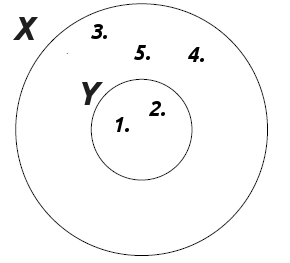
$X$ ve $Y$ aynı evrensel kümede bulunan iki küme ve
- $X\backslash Y'= \{ 1,2 \}$
- $X\backslash Y= \{ 3,4,5 \}$
- $X \cup Y=\{1,2,3,4,5 \}$
ise $Y$ kümesini yazınız?
ifadeleri incelersek;
$X\backslash Y'= \{ 1,2 \}$ ise $X$'in $Y$'nin dışındaki elemanlardan farklı olan elemanları $1$ ve $2$'dir.
$Y=\{1,2 \} $
aşağıdaki şekle bakıldığında daha rahat anlaşılabilir.
- $E = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 \}$
- $A = \{ 1, 2, 3, 4, 5 \}$
- $B = \{1 , 2 , 5 , 6, 7 \}$
- $C = \{ 2, 5, 6, 9 \}$
yukarıdakilere göre, $ B $ — $ (A' \cup C') $ kümesini yazınız.
$A'= \{6,7,8,9,10 \}$
$C'=\{1,3,4,7,8,10 \}$
$ (A' \cup C')=\{1,3,4,6,7,8,9,10 \} $
$ B $ — $ (A' \cup C')=\{2,5\} $
- $A = \{ 1, 2, 3, 4 \}$
- $A\cup B = \{ 1, 2, 3, 4, 5 , 6, 7 \}$
- $A $ — $ B=\{1 ,2 , 3 \}$
yukarıdakilere göre, $ B $ kümesini yazınız.
$A $ — $ B=\{1 ,2 , 3 \}$ olduğuna göre $4$ hem $A$ hem de $B$ kümelerinde bulunmalıdır.
$A\cup B = \{ 1, 2, 3, 4, 5 , 6, 7 \}$ olması için $B$ kümesinde $ \{5,6,7 \}$ elemanları bulunmalıdır. Ortak eleman olan $4$'ü de eklersek
$B=\{4,5,6,7\}$ olur.
- $A\cup B = \{ a, b, c, d, e \}$
- $C= \{a, d , e, f, g, h \}$
olduğuna göre, $ (A \cap C) \cup (B \cap C) $ kümesini yazınız.
$ (A \cap C) \cup (B \cap C) $ ifadesini $ ( A \cup B) \cap C$ şeklinde de ifade edebiliriz.
Buna göre cevap $\{ a, d , e \}$'dir.
- $A = \{ 1, 12, 13, 15 \}$
- $B = \{ 2, 3, 4, 6 \}$
- $C=\{ 2 , 5, 13, 15 \}$
yukarıdakilere göre, aşağıdakilerden hangisi doğrudur.
- $ A \cap C= \emptyset $
- $A $ — $ B=\emptyset$
- $C $ — $ B=C$
- $ B \cap C= \emptyset$
- $B $ — $ A=B$
$ A \cap C= \emptyset $ doğru değildir, $A$ ve $C$'nin ortak elemanları vardır, $13$ ve $15$ ortak elemanlarıdır.
$A $ — $ B=\emptyset$ ifadesi de doğru değlidir, $A$'nın $B$'den farklı elemanları vardır.
$C $ — $ B=C$ ifadesinin doğru olması için $ C \cap B$'nin $ \emptyset$ olması gerekirdi, halbuki ortak elemanları vardır, $2$ ortak elemanlarıdır.
$2$ ortak elemanlarıdır yukarıda söylemiştik, $ B \cap C$ boş küme olamaz.
$B $ — $ A=B$ doğrudur, çünkü $B$ ile $A$'nın ortak elemanı yoktur, $B \cap A= \emptyset $'dir.
$A$ ve $B$ aynı evrensel kümedeki iki kümedir.
$(A$ — $ B')$ — $ A$
kümesini yazınız.
$B$ , $A$'nın altkümesi olsun ya da olmasın $(A$ — $ B')$ ifadesinde, eğer $A$ boş küme değilse, $A$'nın elemanları olmalıdır. .Bu durumda $(A$ — $ B')$ ifadesinin $A$'dan farklı elemanları olamaz. $(A$ — $ B')$ — $ A$ ifadesinin eşiti bu durumda $\emptyset$ olmalıdır.
$ C \cap B =\emptyset $ olduğuna göre
$\left[ C\cup (C\cup B)' \right] '$
kümesini yazınız.
Belirtilmediğine göre evrensel kümemiz $C$ ve $B$ kümelerinin birleşiminden oluşmaktadır. Buna göre $(C\cup B)$'nin değili boş kümedir. $C\cup \emptyset $ $C$ de $C$ olacaktır.
bu durumda ifademiz $C'$ haline gelmiştir. $ C \cap B =\emptyset $ olduğuna göre $C'$ $B$ kümesine eşittir. Yani cevabımız $B$'dir.
$ A \text{ ve } B $ kümelerinin tümleyenleri $A', B'$ ise
$(B $ — $ A)\cap (A$ — $ B)$
kümesini yazınız.
$B $ — $ A$ , $B$ kümesinde olup $A$'da olmayanları ifade eder. Aynı şekilde $A $ — $ B$ , $A$'da olup $B$'de olmayanları ifade eder. Bu durumda bu iki ifadenin kesişme imkanı tanım gereği yoktur, cevap $\emptyset $'dir.
$ A$ ve $B \neq \emptyset$ ve
$B\cap A'$ neye eşittir.
$B$ — $(B\cap A)$ 'ya eşittir.
$A\neq \emptyset $ ve $A\subset C$ ise
$(A\cup \emptyset) \cup (A \cap C) $
ifadesine şıklardan hangisine eşittir?
- $ A $
- $\emptyset $
- $A'$
- $C/A$
- $C$
$(A\cup \emptyset) =A$'dır, $A \cap C$ ise $A$, $C$'nin altkümesi olduğuna göre $A$'dır, bu iki ifadenin birleşimi de $A$'dır, doğru cevap $a$ şıkkıdır.
$E$ evrensel küme olmak üzere, $A$ ve $B$ kümeleri verilmiştir.
$A\subset B$ ise, hangi şık yanlıştır?
- $ A\cap B=A $
- $B'\subset A'$
- $B' \cap A=\emptyset$
- $A\cup B=B$
- $B\cap A'=A$ — $ B$
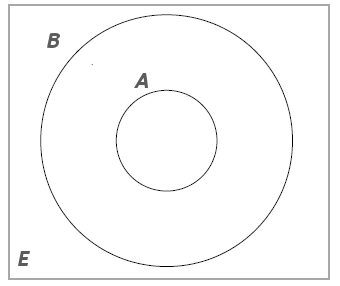
Aşağıdaki şemaya bakarsak rahatça görebileceğimiz gibi;
$B$, $A$'yı kapsadığından ilk ifade doğrudur.
$A$'nın tümleyeni $B$'nin tümleyenini kapsar, ifade doğrudur.
$B'$, $A$ ile kesişmez, ifade doğrudur.
$A$, $B$'nin altkümesi olduğu için $A$ ile $B$'nin birleşimi $B$'dir, ifade doğrudur.
$B \cap A'$ ifadesinin eşiti ise $B$ — $A$ olmalıydı, ifade yanlıştır.
$E$ evrensel küme olmak üzere, $A$ ve $B$ kümeleri verilmiştir.
$(B$ — $ A)\cup (B'$ — $ A)$ kümesi şıklardan hangisine eşittir?
- $ A\cup B' $
- $B'$
- $A\cup B$
- $A'\cap B$
- $A'$
$A\neq B\neq C$ olmak üzere,
$A\subset B\subset C$ ve
$(A\cup B)' \cap (B\cup C)'$ kümesi neye eşittir?
- $ B$
- $A$
- $C$
- $C'$
- $\emptyset$
$(A\cup B)'$ ifadesi $A'$ ya dolayısıyla boş kümeye eşittir, $(B\cup C)'$ ifadesi ile $\emptyset $ kesişimi ise yine boş kümedir. Cevap $e$ şıkkıdır.
$C\subset B \subset A$ olmak üzere,
$(A'\cap B') \cap (B' \cap C')$ neye eşittir?
- $C' $
- $C$
- $\emptyset$
- $A'$
- $B'$
$(A'\cap B')$ ifadesi $B \subset A$ olduğu için boş kümeye eşittir.$ B' \cap C'$ ise $B \subset C$ olduğu için yine boş kümedir. İfademiz $ \emptyset \subset \emptyset $ dönüştüğü için cevap $\emptyset $'dir.
$E$ evrensel küme olmak üzere,
$E=\{x|x\in N \qquad 1\leq x \leq 10 \}$
\[ A=\{1, 2, 3, 4, 5\} \text{ ve } B=\{1, 2, 5, 7, 8, 9, 10\} \]
$C'=\{ 2, 5, 7, 9 \}$ ise
$A$ — $ (B\cap C)$ kümesini yazınız.
$E$ evrensel kümemiz $1,2,3,4,5,6,7,8,9,10$ elemanlarından oluşmaktadır.
$C'=\{ 2, 5, 7, 9 \}$ ise $C$ kümesinin elemanları $1, 3, 4, 6, 8, 10$'dur, bu durumda $ (B\cap C)$, $ \{1, 8, 10 \}$'dur.
$A$ — $ \{1, 8, 10 \}$ ise $\{2,3,4,5 \} $'tir.
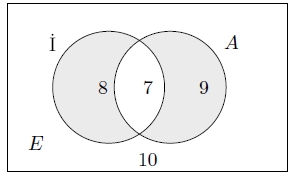
- E: Bir sınıftaki tüm öğrenciler
- İ: İngilizce bilmeyen öğrenciler
- A: Almanca bilmeyen öğrenciler
bunlara göre aşağıdakilerden hangisi yanlıştır?
- Bir dil bilen sayısı 17'dir.
- İki dili de bilenlerin sayısı 10'dur.
- İki dili de bilmeyenlerin sayısı 7'dir.
- En fazla bir dili bilenlerin sayısı 27'dir.
- En az bir dil bilenlerin sayısı 27'dir.
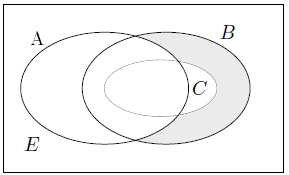
taralı alan şıklardan hangisi ile ifade edilemez?
- $A'\cap C' \cap B$
- $B\cap (C\cup A)'$
- $(A\cap B)' \cap C'$
- $(B $ — $ A)$ — $ C$
- $(B $ — $ C)\cap A'$
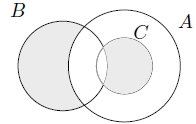
taralı bölgeleri aşağıdakilerden hangisiyle ifade edebiliriz?
- $(A$ — $ B) $ — $ (B\cap C) \cup (B$ — $ A)$
- $(A'\cap B) \cup C$
- $(B$ — $ A)\cap (A'$ — $ C) $
- $(B$ — $ A)\cup(C$ — $ B)$
- $ (A'\cap B) \cup (A'\cap C) $





