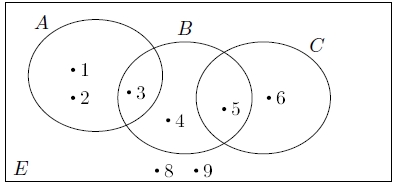
yukarıdakilere göre,
$ C$ — $ (A\cap B') $ kümesi şıklardan hangisidir?
- $ \{ 5,6,8,9 \} $
- $ \{ 6 \} $
- $ \{ 3,5,6 \} $
- $ \{ 4,5,6 \} $
- $ \{ 5, 6\} $
$A\cap B' $ ifadesi $B$'nin dışında olan ama $A$'da olan elemanları gösterir. Yani $1$ ve $2$ elemanlarını. $C$'nin bu elemanlardan farklı elemanları ise zaten $C$'nin kendisidir, yani cevap $ \{5,6 \} $ olmalıdır.
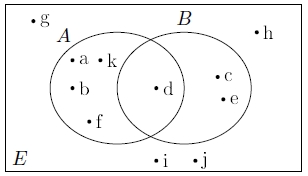
yukarıdakilere göre,
$ (A$ — $ B)' $ — $ A $ kümesi şıklardan hangisidir?
- $ \{c, e, g, h, i, j \} $
- $ \{d,g,i,j\} $
- $ \{c,d,e \} $
- $ \{c, e, g,i,j \} $
- $ \{c, d, e, g, i, j \} $
- $ \{c, d, i\} $
$ (A$ — $ B) $ ifadesi $A$'da olup $B$'de olmayan elemanları ifade eder, yani $ {a,b,f,k}$ elemanlarıdır, bunun
tümleyeni ise, bu elemanlar hariç $E$'de bulunan tüm elemanlardır, yani $(A$ — $ B)' = \{ c,d,e,g,h,i,j \} $'dir , bundan da $A$'daki elemanları çıkarırsak, $ (A$ — $ B)' $ — $ A = \{c,e,g,h,i,j \}$ cevabına ulaşırız.
$A$ ve $B$ , $E$ evrensel kümesinin birbirinden farklı alt kümeleridir.
Buna göre önermelerden hangileri her zaman doğrudur?
- $ B\subset A \Rightarrow B\cap A=A $
- $ B\subset A \Rightarrow A'\subset B' $
- $ B'= A \Rightarrow s(B $ — $ A)+ s(A $ — $ B)= s(A\cup B)$
- $ A\subset B \Rightarrow s(A)\lt s(B) $
- $ A\cup B=B \Rightarrow A\subset B $
Önermeleri tek tek inceleyelim:
- $ B\subset A \Rightarrow B\cap A=A $
$B$ $A$'nın altkümesi ise $B$ kesişim $A$ $B$'ye eşit olmalıydı, çünkü $B$'nin tüm elemanları $A$'nın da elemanıdır ama $A$'nın $B$'den farklı elemanları da bulunabilir. İfade yanlıştır doğrusu $ B\subset A \Rightarrow B\cap A=B $ olmalıydı.
- $ B\subset A \Rightarrow A'\subset B' $
$B$ $A$'nın altkümesi ise aşağıdaki şekillerden de görülebileceği üzere $B$'nin tümleyeni (yeşile boyanmış) $A$'nın tümleyenini (maviye boyanmış) kapsar. İfade doğrudur.
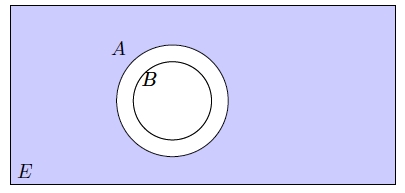
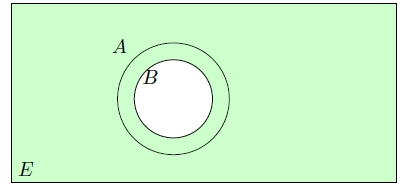
- $B'= A \Rightarrow s(B $ — $ A)+ s(A $ — $ B)= s(A\cup B)$
ifadeyi incelersek $B'= A$ ise $ B\cap A= \emptyset $'dir. Bu iki küme kesişmiyorsa $B $ — $ A=B$ ve $A $ — $ B=A$ olur, bu durumda iki kümenin birleşiminde ortak eleman olamayacağı için iki kümenin birleşiminin eleman sayısı, eleman sayılarının toplamı olacaktır, ifade doğrudur.
- $ A\subset B \Rightarrow s(A)\lt s(B) $
$A=B$ durumunda bu ifade doğru değildir, her küme kendisinin altkümesidir.
- $ A\cup B=B \Rightarrow A\subset B$ ifadesi doğrudur, çünkü $A$'nın her elemanı $B$'nin elemanıdır ve $A$'nın $B$ dışında kalan elemanı yoktur. Yani $A$ $B$'nin altkümesidir.
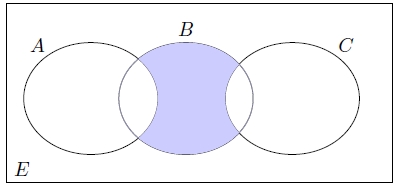
taralı alanı hangi şık ifade eder?
- $ B$ — $ (A\cup C) $
- $ (A\cup C) $ — $ B' $
- $ (A\cup B\cup C)' $
- $ B$ — $(A\cap C) $
- $ (A\cup C)' $
$a$ şıkkı doğrudur, şekilde de görüldüğü gibi taralı alan $B$'nin $A \cup C$'den farkıdır.
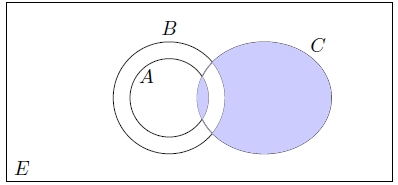
taralı alanları hangi şık ifade eder?
- $ (B$ — $ A)\cup C $
- $ (B$ — $ A)\cap C $
- $ C $ — $ (A\cap B)$
- $ (C$ — $ B) \cup (B$ — $ A) $
- $ (C$ — $ B) \cup (C\cap A) $
Taralı alanlardan sağ taraftaki $ (C$ — $ B)$ ile ifade edilir, sol taraftaki küçük taralı alan ise $C \cap A$ ile ifade edilir, cevap $e$ şıkkıdır.
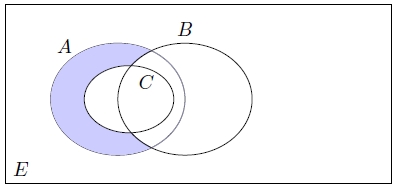
taralı alanları hangi şık ifade eder?
- $ A'\cap C' \cap B $
- $ (A$ — $ B)\cup(C$ — $ B) $
- $ (A$ — $ B)\cap B' $
- $ (A$ — $ B)\cup (A$ — $ C) $
- $ B'\cup(A$ — $ C) $
Şekilden de görülebileceği taralı alan $B$'nin tümleyeni ile $A$ — $ C$'nin kesişimidir. Doğru cevap $e$'dir.
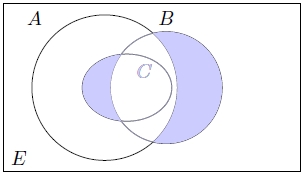
taralı alanları hangi şık ifade eder?
- $ (A$ — $ B)\cup(A\cap C) $
- $ (C$ — $ B) \cup A' $
- $ (B'\cap C)\cup A' $
- $ (A\cap C)\cup (B$ — $ A) $
- $ (C$ — $ B)\cup (B$ — $ A) $
Taralı alanın sol tarafı $C$'nin $B$'den farkıdır, sağ taraftaki taralı alan ise $B$'nin $A$'dan farkıdır, doğru cevap $e$'dir.
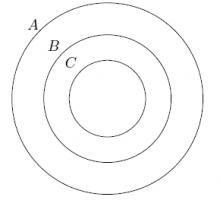
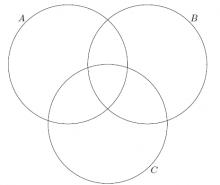
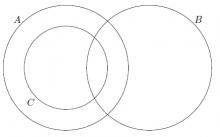
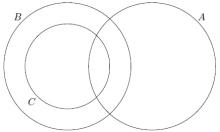
$4$, $8$ ve $32$ sayılarının pozitif tam bölenlerinin kümesi sırası ile C, B ve A kümeleri ise bu kümeler hangi şıkta doğru gösterilmiştir?
- .
- .
- .
- .
- .
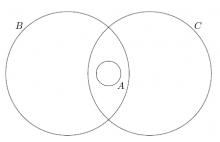
$32$'nin tam sayı bölenleri $ \{ 1,2,4,8,16,32 \}$'dir, $8$'in ise $ \{ 1,2,4,8 \}$, $4$'ün de $ \{1,2,4 \}$'tür. Bu durumda $C\subset B\subset A$'dir. Doğru cevap $a$'dır.
$A=[-5,3)$ ve $B=(0,7)$ kümeleri için
$A\cap B'$ kümesi nedir?
$B'=( -\infty , 0] \cup [7, + \infty]$'dir.
$A\cap B'=[-5,0]$ olur.
$A=[-5,7)$ ve $B=[5,8]$ kümeleri için
$A\cap B'$ kümesi nedir?
$B'=( -\infty , 5) \cup (8, + \infty)$'dir.
$A\cap B'=[-5,5)$ olur.
- $A= \{ x:x\in \mathbb{R}, |x|\lt 5 \}$
- $B= \{ x:x\in \mathbb{R}, |3x+3|\lt 6 \}$
kümeleri veriliyor.
$A$ — $ B$ kümesi nedir?
$A=(-5,5)$ aralığındadır. Paranteze dikkat edelim, $-5$ ve $5$ $A$'nın elemanları değildir.
$B$ ise $|3x+3|\lt 6$ eşitliğini sağlayan $ (-3,1) $ aralığıdır.
$(A$ — $B)= (-5,-3] \cup [1,5)$ kümesidir.
- $A= \{ x:x\in \mathbb{R}, |x|\lt 8 \}$
- $B= \{ x:x\in \mathbb{R}, |2x+5|\lt 7 \}$
kümeleri veriliyor.
$A\cap B$ kümesi nedir?
$A=(-8,8)$ aralığı kümesidir.
$B=(-6,1)$ aralığı kümesidir. $A\cap B$ ise $B$'nin tümüdür.
$A\cap B = (-6,-1)$ aralığıdır.
- $A= \{ x:x\in \mathbb{R}, |x|\lt 6 \}$
- $B= \{ x:x\in \mathbb{R}, |3x-4|\lt 8 \}$
kümeleri veriliyor.
$A\cup B$ kümesi nedir?
$A= (-6,6)$ ve $B=(-2,3)$ aralıkları ile ifade edilebilir.
Bu durumda $B\subset A$'dır. $A\cup B=A$'dır.













