$A$ ve $B$ kümeleri için:
$2s(A$ — $ B)=3s(A\cap B)=s(A\cup B)$
$A$ — $ B$ kümesinin kaç elemanı vardır?
$A$ ve $B$ kümeleri için:
$s(A$ — $ B')=3$ ve $A$ kümesinin alt küme sayısı $32$,
$s(A\cup B)=10$ ise $B$ kümesinin kaç elemanı vardır?
$B$ kümesinin tümleyeni $B$'nin dışındaki elemanları gösterir, $A$ kümesinin $B$'nin dışındaki elemanlardan farklı bir elemanı olabilmesi için bu elemanların $B$'nin içinde olması gerekir.
$(A$ — $ B')= A\cap B$ 'dir. Bu durumda $A\cap B$'de $3$ ortak eleman olmalıdır.
$A$ kümesinin altküme sayısı $32 =2^5$ olduğundan $A$'nın eleman sayısı $5$'tir. Şekilde görüldüğü gibi $s(A$ — $B)=2$ olmalıdır, $s(A\cup B)= s(A$ — $B) + s(A\cap B) + s(B$ — $A)$ olduğuna göre $B$'nin $A$'dan farklı $5$ elemanı bulunmalıdır. $s(B) = 8 $ olur.
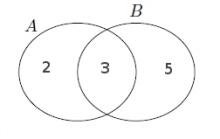
$A$ ve $B$ kümeleri için
- $s(A$ — $ B')= 2$
- $A$ kümesinin alt küme sayısı 64
- $s(A\cup B)=16$
olduğuna göre $s(B)$ kaçtır?
$s(A$ — $ B')=s(A\cap B)= 2$'dir$A$ kümesinin altküme sayısı $64$ ise $n$ elemanlı bir kümenin altküme sayısı $2^n$ olduğuna göre, $A$'nın eleman sayısı $6$ olur. $s(A\cup B)= s(A$ — $B) + s(A\cap B) + s(B$ — $A)$ olduğuna göre $B$'nin $A$'dan farklı $10$ elemanı bulunmalıdır. Ortak elemanları da eklersek $s(B)=12$ olur.
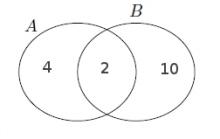
- $A= \{ 1,\{2,3 \} \}$
- $B=\{ 2,3 \}$
kümelerinin kuvvet kümeleri $P(A)$ ve $P(B)$'dir
buna göre $P(A)\cap P(B)$ kümesini yazınız.
Kuvvet kümesi bir kümenin bütün alt kümelerinin kümesidir. İki kümenin ortak elemanı olmadığı için ortak alt kümeleri sadece boş kümeyi içeren alt kümedir.
$P(A)\cap P(B)=\{ \subset \}$ 'dir, dikkat ediniz sadece $\subset$ değil, elemanı boş küme olan kümedir.
$A$ ve $B$ kümeleri için
- $A\cup B$'nin alt küme sayısı 256,
- $A\cap B$ 'nin alt küme sayısı 8,
- $A$ — $ B$ 'nin alt küme sayısı ise 16'dır.
$B$ — $ A$ kümesi kaç elemanlıdır?
$A\cup B$'nin eleman sayısı $2^8$ altkümesi olduğuna göre $8$'dir. $A\cap B$'nin eleman sayısı da $2^3$ altkümesi olduğuna göre $3$'tür. $A$ — $ B$'nin ise $2^4$ altkümesi olduğuna göre $4$ elemanı vardır.
$s(A\cup B)= s(A$ — $B) + s(A\cap B) + s(B$ — $A)$ olduğuna göre, $s(B$ — $A)=1$ olur.
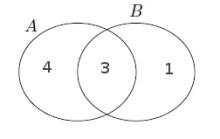
- $A\cup B$'nin alt küme sayısı 128'dir.
- $s(A$ — $ B)=5$ ise
$B$ kümesinin kaç elemanı vardır?
$A\cup B$'nin alt küme sayısı 128 ise , $A\cup B$'nin eleman sayısı $2^n=128$ $n=7$ , $7$'dir.
$s(A\cup B)=7$ ve $s(A$ — $ B)=5$ ise, $B$'nin eleman sayısı $7-5=2$'dir.
- $s(A$ — $ B)=7$
- $s(B$ — $ A)=12$
- $A\cap B$ kümesinin özalt küme sayısı 15
ise, $s(A\cup B) $ kaçtır?
$A\cap B$ kümesinin özalt küme sayısı 15 ise alt küme sayısı $16$'dır.
Eleman sayısı ise $2^n=16$ $n=4$'ten $4$'tür.
şimdi kümelerimizi grafikte de görebileceğimiz gibi cevabı bulabiliriz.
$s(A\cup B)=7+4+12=23 $

Alt küme sayısı $n$ olan bir $A$ kümesinin eleman sayısı $5$ artırılırsa, alt küme sayısı kaç artar ?
Alt küme sayısı $2^n$ dir, $5$ eleman artırılırsa $2^{n+5}$ olur.
\begin{align*}
2^{n+5}-2^n&=2^5\cdot 2^n-2^n\\
&=2^n(2^5-1)\\
&=31\cdot 2^n \\
\end{align*}
kadar artar...
Alt küme sayısı ve özalt küme sayısı toplamı $127$ olan bir kümenin 2 elemanlı kaç tane alt kümesi vardır?
Özalt küme sayısı $127$ ise alt küme sayısı $128$, eleman sayısı $2^n=128=2^7$'den $7$'dir.
$2$ elemanlı alt küme sayısı $\binom{5}{2}$ li kombinasyonudur.
\begin{align*}
\binom{5}{2}&= \frac{5!}{(5-2)! \cdot 2!}\\
&= \frac{5!}{3! \cdot 2!}\\
&=\frac{5\cdot 4\cdot 3\cdot 2\cdot 1}{3\cdot 2\cdot 1\cdot 2\cdot 1}\\
&= \frac{5\cdot 4}{2\cdot 1}\\
&=10
\end{align*}
$A$ ve $B$ gibi iki kümenin alt küme sayıları toplamı $40$'tır. Buna göre bu iki kümenin eleman sayıları toplamı kaçtır?
Toplamı $40$ olan $2$'nin kuvvetleri sadece $2^5=32$ ve $2^3=8$ vardır, $s(A) + s(B)=5+3=8$'dir.
$A= \{ 1,2,3,4,5 \}$ kümesinin $2$ ve $5$'i beraber bulundurmayan kaç tane alt kümesi vardır?
$A$'nın tüm alt kümelerinin sayısı $2^5=32$'dir, şimdi tersten düşünüp $A$'nın $2$ ve $5$'i beraberce bulunduran alt küme sayısını bulalım,
$2$ ve $5$ hep bulunuyorsa geriye $1,3,4$'ten oluşan bir küme kalıyor, bu üç elemandan oluşan kümenin alt küme sayısını bulursak, $2$ ve $5$ sabit yanlarına konulacağı için $2$ ve $5$'i beraberce her zaman bulunduran alt küme sayısını bulmuş oluruz. $1,3,4$'ten oluşan kümenin alt küme sayısı $2^3=8$'dir, $32-8=24$ ise $2$ ve $5$'i beraber bulundurmayan alt küme sayısıdır.
Bir $A$ kümesinin $2$ elemanı atıldığında elde edilen kümenin alt kümelerinin sayısı, $A$ kümesinin alt kümelerinin sayısının yüzde kaçıdır?
$A$ kümesinin eleman sayısına $n$ diyelim, $2^n$ alt küme sayısı, $2$ eleman atıldığında alt küme sayısı $2^{n-2}$ olur.
Bunların birbirine oranına bakalım.
\begin{align*}
\frac{2^n}{2^{n-2}}&= \frac{2^n}{2^n \cdot 2^{-2}}\\
&=\frac{2^n\cdot 2^2}{2^{n}} \qquad \text{ $2^{-2} $ yukarıya $2^2$ olarak geçer. } \\
&=4\\
\end{align*}
$2$ eleman atıldığında alt küme sayısı $\frac{1}{4}$'üne düşüyor, bu da $\%25$'e eşittir.
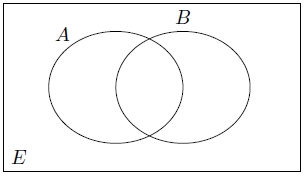
$E$ evrensel kümesinde,
- $s(E)=40$
- $s(A\cap B)\neq \emptyset$
- $s(A\cup B)'=18$
- $s(A) \gt s(B)$
ise $B$ kümesinin eleman sayısı en çok kaç olabilir?
$n$ elemanlı bir kümenin en çok $n-3$ elemanlı alt küme sayısı $42$ olduğuna göre $n$ kaçtır?
- $A \not\subset B$
- $A\cap B \neq \emptyset$
- $s(A$ — $ B)=10$
olduğuna göre $s(A\cup B)$ en az kaç olabilir?
$A= \{ 0, 1, \{1,2 \}, 3, \{2,3 \}, 4 \}$ kümesinin alt kümelerinin kaçında $1$ ve $3$ elemanları birlikte bulunur?
$A= \{ a,b,c,d,e,f,g \} $ kümesinin $3$ elemanlı alt kümelerinin kaç tanesinde $a$ bulunur $e$ bulunmaz?
Bir $A$ kümesinin kuvvet kümesinin alt kümelerinin sayısı 128 olduğuna göre, $A$ kümesinin $2$ elemanlı kaç alt kümesi vardır?
Bir $A$ kümesinin 3 elemanlı alt kümelerinin sayısı $84$ olduğuna göre, $2$ elemanlı alt kümelerinin sayısı kaçtır?





