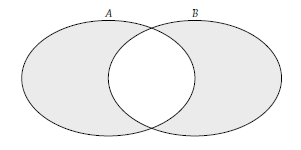
Evrensel Küme ve Tümleme
Belli bir problemdeki tüm elemanları içeren kümeye evrensel küme diyeceğiz ve bu kümeyi $E$ ile göstereceğiz.
Bir $A$ kümesinde olmayan ancak evrensel kümede olan tüm elemanlardan oluşan kümeye $A$ nın tümleyeni denir ve $A'$ şeklinde gösterilir.
\[ A' = \{ x | x \not \in A \} \]
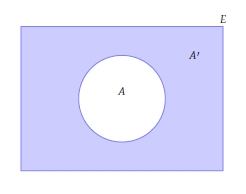
$A$ nın tümleyeni $A$ da olmayan tüm elemanları içerdiğinden şu iki sonuç açıktır:
- $A \cap A' = \emptyset $
- $A \cup A' = E $
De Morgan Kuralları
Birleşim ve kesişim işlemlerinde tümleyen işleminin şu iki özelliği vardır:
- $(A \cup B)' = A' \cap B'$
- $(A \cap B)' = A' \cup B'$
Örnek
Bileşme, Kesişme, Fark ve Simetrik Fark
- Bileşim
- Değişme Özelliği
- Tek Kuvvet Özelliği
- Birleşme Özelliği
- Kesişim
- Fark
İki kümenin elemanlarının tümünden oluşan kümeye bileşim kümesi denir ve $ A \cup B $ şeklinde gösterilir. Bileşim kümesindeki elemanlar $A$ ve $B$ nin en az birinde olmak zorundadırlar. Bunu şöyle de gösterebiliriz.
\[ A \cup B = \{ x | x \in A \vee x \in B \} \]
$x$ öyle ki $x$ elemanıdır $A$ veya($ \vee $) $x$ elemanıdır $B$.
$ A $ ve $ B $ iki farklı küme olmak üzere bileşim kümesi Venn şeması ile aşağıdaki gibi gösterilebilir.
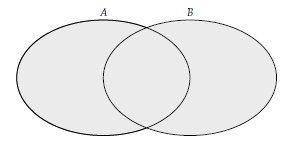
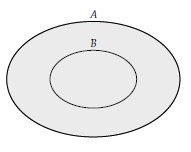
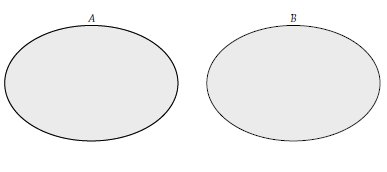
- Bileşim işleminin özellikleri
$ A \cup B = B \cup A $
$ A \cup A = A $
$ A \cup (B \cup C) = (A \cup B) \cup C $
Örnek
$ A = \{ 2,3,4,5 \} $ ve $B = \{ 3,4,7 \}$ olmak üzere $ A \cup B$ kümesini liste yöntemi ile yazınız.
Çözüm
İki kümedeki elemanların tamamını birleşim kümesine atıyoruz ve tabii ki küme tanımından dolayı aynı elemanı birden fazla kere koymuyoruz.
\[ A \cup B = \{ 2,3,4,5,,7 \} \]
Görüldüğü gibi bileşim kümesinin eleman sayısı iki kümenin eleman sayıları ile aynı olmayabilir. Kesişen kümeler ise ortak elemanları iki kere koyamayacağımızdan bileşim kümesinin eleman sayısı kesişim kadar azalır. Bir $A$ kümesinin eleman sayısı $s(A)$ şeklinde gösterilir. Bileşim kümesinin eleman sayısı \[ s(A \cup B) = s(A) + s(B) - s(A \cap B) \]
İki kümenin ortak elemanlarından oluşan kümeye kesişim kümesi denir ve $ A \cap B $ şeklinde gösterilir. Kesişim kümesindeki elemanlar $A$ ve $B$ nin ikisinde de olmak zorundadırlar. Bunu şöyle de gösterebiliriz.
\[ A \cap B = \{ x | x \in A \wedge x \in B \} \]
$x$ öyle ki $x$ elemanıdır $A$ ve($ \wedge $) $x$ elemanıdır $B$.
$ A $ ve $ B $ iki farklı küme olmak üzere kesişim kümesi Venn şeması ile aşağıdaki gibi gösterilebilir. 
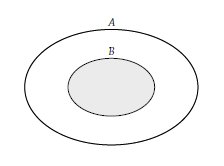
Bir $A$ kümesinin başka bir $B$ kümesinde olmayan elemanlarını göstermek için $A$ nın $B$ den farkı anlamında $ A \backslash B$ ya da $A-B$ kullanılır ve Venn şeması gösterimi şöyledir.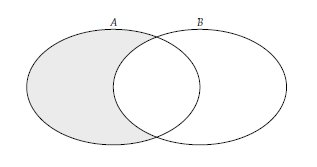
Örnek
Verilen $A$ ve $B$ kümeleri için $A \backslash B$ kümesini bulunuz.
- $ A = \{ 1,3,5,7,9 \}$ ve $ B = \{ 1,2,3,4,5 \} $
- $ A = \{ 1,3,5,7,9 \}$ ve $ B = \{ 1,3 \} $
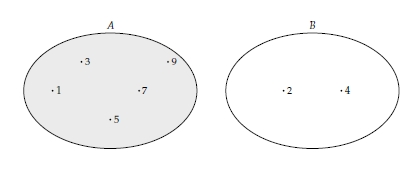
- $ A = \{ 1,3,5,7,9 \}$ ve $ B = \{ 2,4 \} $
Çözüm
- $A$ da olup $B$ de olmayan elemanlarla bir küme oluşturursak, $ A \backslash B = \{ 7,9 \} $
- $ A \backslash B = \{ 5,7,9 \} $
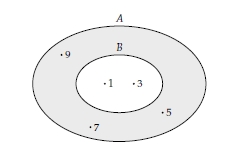
- $ A \backslash B = \{1,3, 5,7,9 \} $
- Simetrik Fark
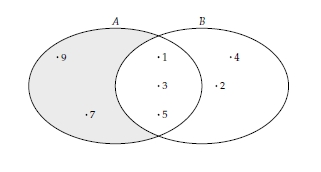
İki kümenin birbirinden farklı elemanlarının oluşturduğu küme ya da $ A \backslash B $ ve $ B \backslash A $ kümelerinin bileşimine simetrik fark kümesi denir ve $ A \Delta B $ şeklinde gösterilir.