Parabol denklemi ya da ikinci dereceden bir fonksiyon bize üç farklı şekilde verilebilir. İnceleyeceğimiz sırayla bunlar :
- x ekseni formatı: a \cdot (x-x_1)\cdot (x-x_2)
- Tepe noktası formatı: a\cdot (x-r)^2+k
- Genel format: ax^2+bx+c
x ekseni formatı
Önce parabolün x eksenini iki farklı noktada kesmesi durumunda neler yapabileceğimize bakalım.
Tüm fonksiyonlar için x eksenini kesmenin ne anlama geldiğini hatırlatalım. x ekseni üstündeki bir noktanın ordinatı 0'dır. Dolayısıyla bize bir y=f(x) fonksiyonunun x eksenini 3'te kestiği söylenirse bunun anlamı grafik (3,0) noktasından geçiyordur. Fonksiyonda x=3 yazdığımızda y=0 çıkmalıdır. Yani f(3)=0'dır.
Bir parabolün x eksenini 1 ve 3 noktalarında kestiğini düşünelim. Bu durumda otomatik olarak şunu yazabiliriz.
y=a(x-1)(x-3) Çünkü biliyoruz ki elimizde bir ikinci derece fonksiyon var ve x=1 ve x=3'te y değerleri 0 oluyor. İkinci derece bir denklem gibi düşünürsek kökleri 1 ve 3 olan bir denklem yazmak istiyoruz.
x eksenini kestiği noktalar verilince denklemi kesin olarak çıkaramıyoruz. Bilmediğimiz bir a parametresi kalıyor. Onu bulmak için de parabolün x eksenini kestiği noktalar dışında herhangi bir noktasına ihtiyacım var. Örneğin grafikteki parabolü düşünelim: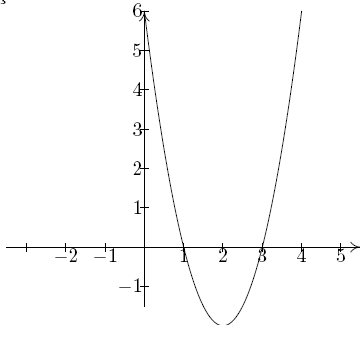
Buradan şu sonucu çıkarabiliriz: Bir parabol x eksenini x_{1} ve x_{2} noktalarında kesiyorsa denlemi: y=a(x-x_{1})(x-x_{2}) şeklinde yazılabilir.
Bir parabol daha düşünelim. Bu sefer x eksenini -1 ve 4 noktalarında kessin ve bir noktası da (1,2) olsun.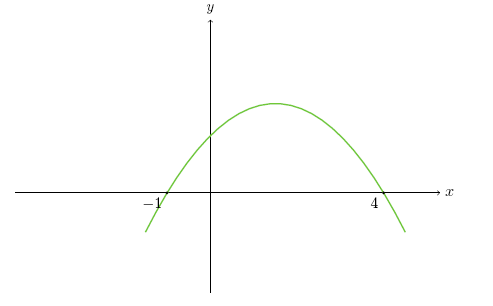 Bu durumda denklem a(x+1)(x-4)=y olur. Verilen diğer noktadan x yerine 1 koyduğumuzda y'nin 2 çıkmasını bekliyoruz. Yerine koyarsak a(1+1)(1-4)=2 olur. Bu denklemden a=\frac{-1}{3} çıkar. Denklemimiz \frac{-1}{3}(x+1)(x-4)=y olur. Burada daha sonra tekrar edeceğimiz bir sonuca dikkat edelim: parabolün kolları aşağı doğru iken a \lt 0 oldu ve parabolün kolları yukarı doğru iken a \gt 0 oldu.
Bu durumda denklem a(x+1)(x-4)=y olur. Verilen diğer noktadan x yerine 1 koyduğumuzda y'nin 2 çıkmasını bekliyoruz. Yerine koyarsak a(1+1)(1-4)=2 olur. Bu denklemden a=\frac{-1}{3} çıkar. Denklemimiz \frac{-1}{3}(x+1)(x-4)=y olur. Burada daha sonra tekrar edeceğimiz bir sonuca dikkat edelim: parabolün kolları aşağı doğru iken a \lt 0 oldu ve parabolün kolları yukarı doğru iken a \gt 0 oldu.
Tepe Noktasının Koordinatları
x eksenini iki farklı noktada kesen bir parabolün görüldüğü gibi bir çukur noktası var. Bu noktanın apsisini nasıl bulabiliriz? Kollar aşağı doğru ise bu nokta bir tepe noktası oluyor. Biz çukur da olsa tepe de bu noktaya Tepe Noktası diyeceğiz ve apsisini \frac{-b}{2a} formülünden bulacağız. Bu formül hemen görebileceğimiz gibi iki kökün tam ortasıdır. İki kök toplamı olan \frac{-b}{a}'yı 2'ye bölerek ortalarını bulmuş oluyoruz. y koordinatı(ordinatı) için de bir formül bulmak istersek \frac{-b}{2a}'yı denklemde yerine koymamız yeterli olur. ax^2+bx+c=a(\frac{-b}{2a})^2+b(\frac{-b}{2a})+c} Buradan tepe noktasının y koordinatının formülü: \frac{4ac-b^2}{4a}=\frac{-\Delta}{4a} çıkar. Bu formülü mümkün olduğunca kullanmayacağız. Tepe noktasının apsisi belli ise yapmamız gereken tek şey parabol denkleminde yerine koyup bize vereceği y değerine bakmaktır.
Toparlarsak: Bir parabolün tepe noktası T'nin koordinatları
x_{t}=\frac{-b}{2a} ve y_{t}=\frac{-\Delta}{4a}
Tepe Noktası Formatı
Bir parabolün tepe noktasının koordinatları verilsin ve bunlar (r,k) olsun. Bu durumda parabol denklemi: {y=a(x-r)^2+k} şeklindedir. Nedenini daha sonra daha iyi anlayacağız. Demek ki tepe noktası verilse de gene bilmediğimiz bir a parametresi var ve bunu bulmak için parabolün bir noktasına daha ihtiyacımız var.
Örnek
Parabolün tepe noktası (1,-4) ve bir noktası(0,-3) olsun.
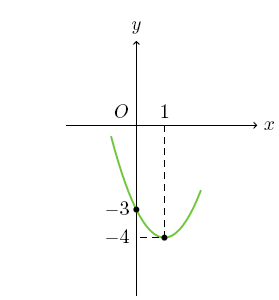 Denklem y=a(x-1)^2+(-4) olur. Parabol (0,-3) noktasından geçtiğine göre x=0 iken y=-3'tür. -3=a(0-1)^2+(-4)\Rightarrow a=1 Yani parabol denklemi y=(x-1)^2-4 ve dağıtırsak x^2-2x-3 olur.
Denklem y=a(x-1)^2+(-4) olur. Parabol (0,-3) noktasından geçtiğine göre x=0 iken y=-3'tür. -3=a(0-1)^2+(-4)\Rightarrow a=1 Yani parabol denklemi y=(x-1)^2-4 ve dağıtırsak x^2-2x-3 olur.
Tepe noktası formatı eksenleri kestiği noktaları bilmiyorsak kullanılabilir. Parabol eksenleri kesmeyebilir!.
Şimdi de aşağıda verilen parabolün grafiğini yazmaya çalışalım: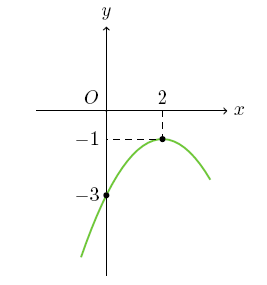 Tepe noktası (2,-1) ve bir nokta (0,-3) tür. y=a(x-2)^2+(-1) ve x=0 için y=-3 tür. Bu değerleri yerine koyarsak a=\frac{-1}{2} ve denklem y=\frac{-x^2}{2}+2x-3 çıkar. Denklemi 2 ile genişletemeyeceğimize dikkat edelim. ikinci derece denklemler konusunda bu tip bir ifade 0'a eşitti burada ise y'ye eşit.
Tepe noktası (2,-1) ve bir nokta (0,-3) tür. y=a(x-2)^2+(-1) ve x=0 için y=-3 tür. Bu değerleri yerine koyarsak a=\frac{-1}{2} ve denklem y=\frac{-x^2}{2}+2x-3 çıkar. Denklemi 2 ile genişletemeyeceğimize dikkat edelim. ikinci derece denklemler konusunda bu tip bir ifade 0'a eşitti burada ise y'ye eşit.
Bu grafikte bir kaç noktaya dikkat edelim. a \lt 0 oldu yani x^2 nin katsayısı negatif oldu ve kollar aşağı doğru. Bunu daha önce işaret etmiştik. Daha sonra inceleyeceğimiz ikinci nokta bu fonksiyon hiç bir zaman 0 olamaz. Çünkü x eksenini kesmiyor. İkinci derece denklemlerden bunun anlamını biliyoruz: \Delta\lt 0. Önemli bir nokta daha var. Bu parabolde x yerine ne yazarsak yazalım y için -1'den büyük bir değer elde edemeyiz. Yani -1 bu fonksiyon için maksimum değerdir. Kollar yukarı doğru olsaydı burası bir minimum değer olacaktı. Tepe noktası hakkında bir şey daha öğrenmiş olduk.
Kolları aşağı doğru olan bir parabol için tepe noktasının ordinatı
bu parabolün maksimum değeri- Kolları yukarı doğru olan bir parabol için tepe noktasının
ordinatı bu parabolün minimum değeridir.
Örnek
y=x^2-6x+4 parabolünün en küçük değeri nedir?Çözüm
Tepe noktasının x koordinatı \frac{-b}{2a}'dan 3 çıkar. 3'ü denklemde yerine yazarsak ordinatı verir. y=3^2-6\times3+4=-5. Cevap -5'tir.Örnek
y=-x^2-2x+a parabolünün en büyük değerinin 5 olması için a ne olmalıdır?Çözüm
Kollar aşağı doğru iken en büyük değer tepe noktasının ordinatıdır. Apsis \frac{-b}{2a}'dan -1 çıkar. Buradan 5=-(-1)^2-2(-1)+a \Rightarrow a=4Hemen burada tepe noktası ve maksimum minimum değer ile ilgili özel bir soru tipini inceleyelim. Yukarıdaki örneklerde parabolün maksimum ya da minimum değeri soruldu bu durumda cevap her zaman tepe noktasının ordinatıdır. Yalnız x için bir aralık verilirse örneğin parabolün [-1,4] aralığındaki minimum değeri nedir denirse konuyu biraz daha anlamak gerekir.
Verilen Bir Aralıkta Parabolün Değer Aralığı
Doğrusal fonksiyonlarda (ax+b şeklindeki fonksiyonlar) x artarken y ya
azalır ya da artar. Örneğin y=-x+5 denkleminin x (1,5) aralığı için değer aralığını (y'nin alacağı değerlerin aralığı) bulalım. Bunun için x=1 ve x=5 yapmam yeterli olur. y=-1+5=4 ve y=-5+5=0 olur. x 1'den 5'e giderken y 4'ten 0'a doğru gitmektedir. Değer aralığı (0,4) olur.
Ancak parabollerde bir sorun var. Parabolde x arttıkça y azalıyorsa tepe noktasından sonra x arttıkça y de artmaya başlar. Aşağıdaki grafik y=\frac{x^2}{4}-x+2 parabolünü göstermektedir.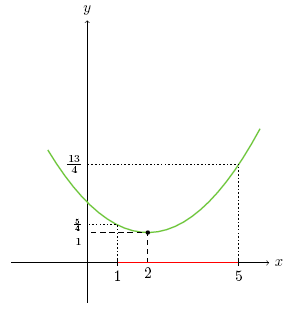 Parabol x -\infty den 2 ye doğru gittikçe azalan y değerleri verir ancak x \gt 2 için y artmaya başlar.
Parabol x -\infty den 2 ye doğru gittikçe azalan y değerleri verir ancak x \gt 2 için y artmaya başlar.
Bu parabolün x\in(1,5) için alabileceği y değerlerini inceleyelim. Aralığın iki ucunu denklemde yerine koyarsak y=\frac{1^2}{4}-1+2=\frac{5}{4} ve y=\frac{5^2}{4}-5+2=\frac{13}{4} buluruz. Ancak y\in(\frac{5} {4},\frac{13}{4}) değildir. Bu parabolün (1,5) aralığında alabileceği en küçük değer x=2 noktasındadır ve 1 dir. Demek ki doğru yanıt y\in(1,\frac{13}{4})'tür. Sonuç olarak: Bir aralık verilip parabolün o aralıkta minimum ya da maksimum noktası sorulursa önce tepe noktasının apsisinin o aralıkta olup olmadığına bakılır. Eğer tepe noktası verilen aralıkta değilse hiç bir sorun yok. Aynen doğrusal fonksiyonlardaki gibi verilen aralığın uçları yazılarak değer aralığı bulunabilir. Ancak böyle bir soru sorulmuşsa %99,9999 tepe noktası verilen aralıktadır. Bu durumda tepe noktasının apsisini ve aralığın tepe noktasına uzak olan ucunu fonksiyonda yerine koyarak değer aralığını buluruz.
Örneğimizde tepe noktası x=2 dedir. Aralığın x=5 noktası tepe noktasına x=1'den daha uzak demek ki y değerleri x=2 ve x=5 için bulacağımız y değeri arasında değişir. 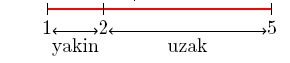
Genel Format
Parabolün genel formatına baktığımızda üç parametre görüyoruz, a, b ve c. Bize doğrusal olmayan üç nokta verildiğinde üç denklemimiz oluyor ve buradan parabolün denklemini çıkarabiliriz. Yani herhangi üç noktası verilen parabolün denklemi yazılabilir her ne kadar hesapların zorluğu verilen noktalara bağlı olsa da.
Örnek
(1,3), (5,3) ve (6,7) noktalarından geçen parabolün denklemi nedir?Çözüm
Denklemimiz y=ax^2+bx+c Verilen birinci noktanın koordinatlarını yerine yazınca 3=a+b+c Verilen ikinci noktanın koordinatlarını yerine yazınca 3=25a+5b+c Verilen üçüncü noktanın koordinatlarını yerine yazınca 7=36a+6b+cİlk iki denklemi birbirine eşitleyince a+b+c=25a+5b+c \rightarrow 24a=-4b \rightarrow b=-6a çıkar. b yerine ikinci ve üçüncü denklemde -6a koyarsak
3=25a-30a+c=-5a+c ve 7=36a-36a+c=c Son denklemden görüldüğü gibi c=7'dir. Bu denklemi -5a+c=3 denkleminde yerine koyarsak a=\frac{4}{5} ve bu değerlerle ana üç denklemimizden birine gidersek b=\frac{-24}{5} buluruz.
