Sinüs Teoremi
Bir $ABC$ üçgeninin açıları $A,B\text{ ve } C$, kenar uzunlukları $a,b,c$ ve çevrel çemberinin yarıçapı da $R$ olsun.
\[\frac{a}{\sin A} = \frac{b}{\sin B}=\frac{c}{\sin C}=2R\]
Önce çevrel çemberi bir kenara bırakıp üçgenin alanını kullanarak teoremi ispatlamaya çalışalım.
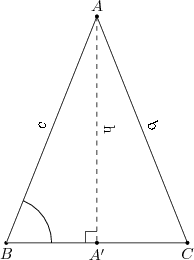
$AA'B$ dik üçgeninde $\frac{h}{c} = \sin \widehat{B}$ dir. Buradan $h=c\sin \widehat{B}$ çıkar. $ABC$ üçgeninin alanı
\[ A(ABC) = \frac{a \cdot h}{2} = \frac{ a c \sin B}{2} \]
Aynı yüksekliği $AA'C$ dik üçgeninden yazsaydık $h= b\sin C$ olacaktı ve $ABC$ nin alanı \[ A(ABC) = \frac{a b \sin C}{2}\]
Anlaşılacağı gibi $b$ veya $c$ kenarına indireceğimiz bir dikme ile de alan
\[ A(ABC)= \frac{b c \sin A}{2} \] Bu durumda alan
\[ A(ABC)=\frac{a b \sin C}{2} = \frac{a c \sin B}{2}=\frac{b c \sin A}{2} \]
$2$ leri sadeleştirip her tarafı $abc$ ile bölüp ters çevirirsek
\begin{align*}
\frac{a b \sin C}{2} = \frac{a c \sin B}{2}=\frac{b c \sin A}{2} \Rightarrow ab\sin C &= ac\sin B = bc\sin A\\
\Rightarrow\frac{ab\sin C}{abc}&=\frac{ac\sin B}{abc} = \frac{bc\sin A}{abc}\\
\Rightarrow\frac{\sin C}{c}&= \frac{\sin B}{b} = \frac{\sin A}{a} \\
\Rightarrow\frac{a}{\sin A}&=\frac{b}{\sin B}=\frac{c}{\sin C}
\end{align*}
Yukarıdaki ispat iki kenar uzunluğu ve aralarındaki açının sinüsü ile alanı bulabileceğimizi gösterdi. Üçgenin çevrel çemberinin yarıçapı $R$ olmak üzere bulduğumuz eşitlik $2R$ ye de eşittir. İkinci ispat yönteminde bunu görebiliyoruz.
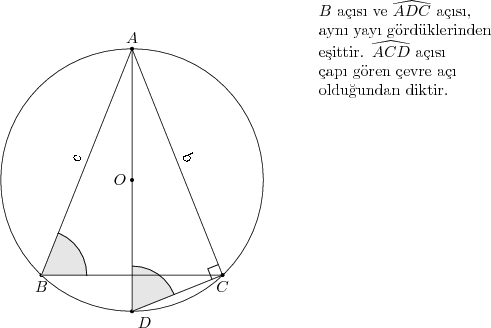
$AD = 2R$ ve $m\widehat{ACD} = 90^{\circ}$ olduğundan $ADC$ dik üçgeninde
\begin{align*}
\sin \widehat{ADC} &= \frac{b}{2R} \\
\frac{b}{\sin\widehat{ADC}}&=2R & \quad \widehat{ADC}&=B \text{ olduğundan}\\
\frac{b}{\sin B} &=2R
\end{align*}
Kosinüs Teoremi
Kosinüs teoremi, pisagor formülünün genel halidir, ya da pisagor, kosinüsün özel bir halidir. Bir üçgenin iki kenarı ve aralarındaki açının kosinüsü ile üçüncü kenar hesaplanabilmektedir:
$ABC$ üçgeninin kenarları $a,b,c$ ve açıları $A,B,C$ olsun:
\begin{align*}
a^2 + b^2 -2ab\cos C &= c^2 \\
b^2 + c^2 -2bc\cos A &= a^2\\
a^2 + c^2 -2ac\cos B &= b^2
\end{align*}
İspat:
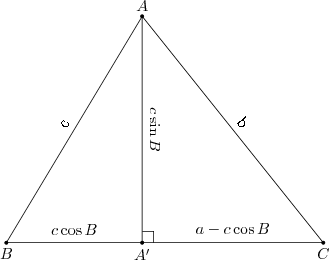
$AA'C$ dik üçgeninde pisagor uygulanırsa:
\begin{align*}
(c\sin B)^2 + (a-c\cos B)^2 &= b^2\\
c^2 \sin^2 B + a^2 -2ac\cos B + c^2 \cos^2 B &= b^2 \\
c^2 (\sin^2 B + \cos^2 B) + a^2 -2ac \cos B &= b^2 & \textit{$\sin^2 x+\cos^2 x=1$ olduğundan}\\
c^2 + a^2 -2ac \cos B &= b^2
\end{align*}
Örnek
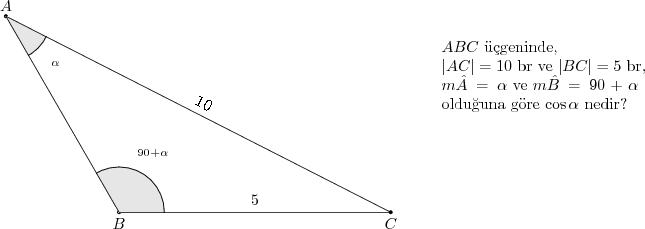
Çözüm
Sinüs teoremi uygulanırsa
\begin{align*}
\frac{|BC|}{\sin \hat{A}} = \frac{|AC|}{\sin \hat{B}} \Rightarrow \frac{5}{\sin \alpha} &= \frac{10}{\sin (90^{\circ}+\alpha)}\\
\frac{5}{10} &= \frac{\sin\alpha}{\sin (90^{\circ}+\alpha)} = \frac{\sin\alpha}{\cos\alpha}\\
\frac{1}{2} &= \tan \alpha
\end{align*}
Örnek
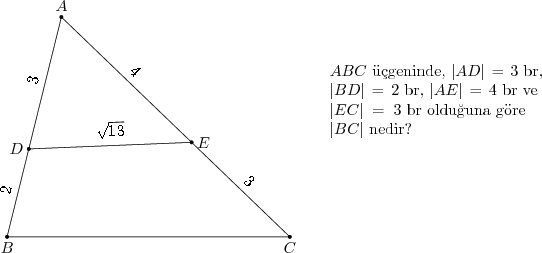
Çözüm
$A$ açısı hem $ADE$ hem de $ABC$ üçgeninin ortak açısıdır. $ADE$ üçgeninin üç kenarı da bilindiğinden $\cos A$ değeri bulunabilir. Buradan da $ABC$ üçgeninde kosinüs teoremi uygulanarak $|BC|$ uzunluğu bulunabilir.
$ADE$ üçgeni için kosinüs teoreminden
\begin{align*}
|AD|^2 + |AE|^2 - 2 |AD||AE|\cos A &= |DE|^2 \\
3^2 + 4^2 - 2 \cdot 3 \cdot 4 \cdot \cos A &= \sqrt{13}^2 \\
25 - 24 \cos A &= 13 \\
\cos A &= \frac{1}{2}
\end{align*}
$ABC$ üçgeni için kosinüs teoremi uygularsak:
\begin{align*}
|AB|^2 + |AC|^2 - 2 |AB||AC|\cos A &= |BC|^2 \\
5^2 + 7^2 - 2 \cdot 5 \cdot 7 \cdot \frac{1}{2} &= |BC|^2 \\
25 + 49 - 35 &= |BC|^2 \\
\sqrt{39} &= |BC|
\end{align*}
Örnek
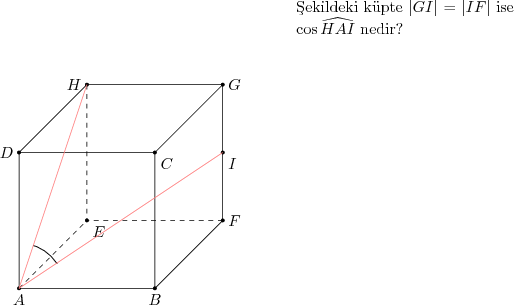
Çözüm
Küpün bir ayrıtının uzunluğu $2$ br olsun. Bu durumda $|GI|=1$ br olacaktır. Verilen açının kosinüsü için yapmamız gereken şey, $AHI$ üçgeninin kenar uzunluklarını bulmak ve kosinüs teoremi uygulamaktır. $AH$ zaten $AEHD$ karesinin köşegenidir ve $2\sqrt{2}$ br olur.
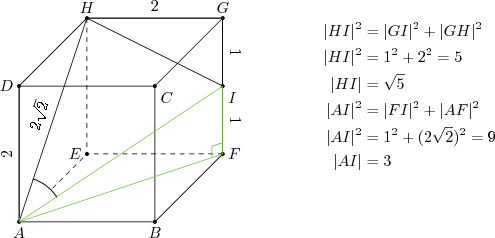
Artık $AHI$ üçgeninin kenarlarını biliyoruz ve istediğimiz açının kosinüsünü hesaplayabiliriz.
\begin{align*}
|AH|^2 + |AI|^2 - 2 |AH||AI|\cos \widehat{HAI} &= |HI|^2 \\
8+9-2\cdot 8 \cdot 3 \cos \widehat{HAI} &= 5\\
\cos \widehat{HAI} &= \frac{1}{4}
\end{align*}
