Tanım ve Görüntü Kümeleri/Tipik Sorular
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
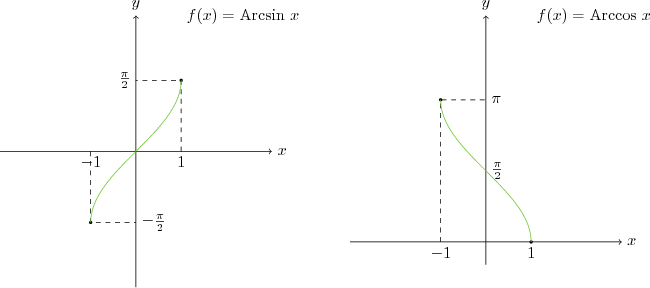
| $arcsin x$ | $-1 \leq x \leq 1 $ | $-\frac{\pi}{2} \leq y \leq \frac{\pi}{2} $ |
| $arccos x$ | $-1 \leq x \leq 1 $ | $ 0 \leq y \leq \pi $ |
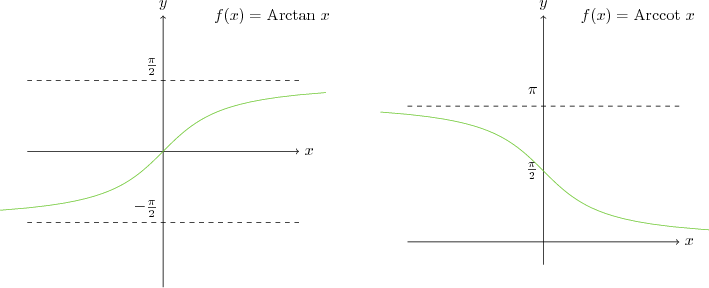
| $arctan x$ | $ \mathbb{R} $ | $-\frac{\pi}{2} \lt y \lt \frac{\pi}{2} $ |
| $arccot x$ | $ \mathbb{R} $ | $ 0 \lt y \lt \pi $ |
Bir fonksiyonun tersi, görüntü kümesi ve tanım kümesinin yerini değiştirir ve asıl fonksiyonun yaptığı eşlemenin tersini yapar. $f(3)=5$ ise fonksiyon $3$'ü $5$'e eşliyordur ve tersi $f^{-1}$'in $5$'i $3$'e eşlemesi gerekir, $f^{-1}(5)=3$.
\begin{align*}
f(3)& \rightarrow 5\\
f^{-1}(5)& \rightarrow 3\\
\end{align*}
Sinüs ve kosinüste tanım kümesi tüm reel sayılardır ancak görüntü kümesi bildiğimiz gibi $[-1,1]$ aralığındadır. Bir fonksiyon ancak bire-bir ve örten ise tersi de fonksiyon olur.
Sinüsün tersini $\sin^{-1}$ ile gösterebiliriz. Sinüs fonksiyonu bir açıyı $[-1,1]$ aralığında bir sayıya eşler, örneğin $\sin \frac{\pi}{6}=\frac{1}{2}$. Ters fonksiyon da $\frac{1}{2}$ yi $\frac{\pi}{6}$ ya eşlemelidir, $\sin^{-1}(\frac{1}{2})=\frac{\pi}{6}$. Ancak sinüsü $\frac{1}{2}$ olan başka açılar da vardır. Bu da ters çevirdiğimizde fonksiyon olmayı engeller, çünkü bir değer iki farklı açıya eşlenmektedir. Bir elemanın iki farklı görüntüsü olamaz. Bu sorunu, ters trigonometrik fonksiyonların görüntü kümesini sınırlayarak çözüyoruz. Sinüs fonksiyonu için bu aralık $-\frac{\pi}{2},\frac{\pi}{2}$ olarak seçilir. Ters trigonometrik fonksiyonları göstermek için yaygın olarak arc ön eki de kullanılır. Yukarıdaki tabloda ters trigonometrik fonksiyonların tanım ve görüntü kümeleri görülmektedir.
Temelde bu fonksiyonları iki tip soru için kullanacağız. Birincisi, sinüs değerinden açıyı anlayacağız. Bu durumda verilen sinüs değeri özel açılardan olacak. İkinci olarak da soru, ters ve normal trigonometrik fonksiyonların bileşkesini içerecek ve bu durumda çoğunlukla bir diküçgen kullanacağız. Aşağıda iki duruma da örnek verilmektedir.
Örnek
$\arcsin\frac{-\sqrt{3}}{2}$ ifadesinin değeri nedir?
Çözüm
Sinüsü $-\frac{\sqrt{3}}{2}$ olan açılardan fonksiyonun görüntü kümesinde olan $-\frac{\pi}{6}$ dır. Verilen ifadede şu dönüşümü yapabilmek de önemlidir:
\[ \arcsin\frac{-\sqrt{3}}{2} = x \Rightarrow \sin x = \frac{-\sqrt{3}}{2} \]
Örnek
$\arctan (-1)= x$ ise $x$ nedir?
Çözüm
Tanjantı $-1$ olan açılar $\frac{\pi}{4}$ ün simetrikleridir ve görüntü kümesi içinde olan açı da $-\frac{\pi}{4}$ tür.
Örnek
$\sin \arccos \frac{1}{3}$ ifadesinin değeri nedir?Çözüm
Bu soru özel açı içermediği için önemlidir. $\arccos \frac{1}{3}$ ifadesinin hangi açı olduğunu bilmiyoruz. Ancak bize zaten bu açı değil, bu açının sinüsü sorulmakta. $\arccos \frac{1}{3}=x$ diyelim.\[ \arccos \frac{1}{3}=x \Rightarrow \cos x =\frac{1}{3}\]
$\arccos \frac{1}{3}=x$ dönüşümünü soruda da yaparsak $\sin x$ in sorulduğu görülür. Bu durumda $x$ in kosinüsü verilmiş ve sinüsü sorulmaktadır. Bir dik üçgen çizelim ve $x$ açısının kosinüsünü $\frac{1}{3}$ yapalım.
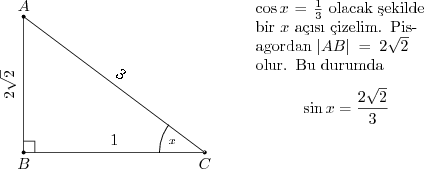
Örnek
$\sin \arcsin \frac{1}{4}$ ifadesinin değeri nedir?Çözüm
Bu, sevilen bir şaşırtmadır. Bir fonksiyon ile tersinin birleşiminin sonucu birim fonksiyondur ve birim fonksiyon da her elemanı kendisiyle eşler. Cevap $\frac{1}{4}$ tür.Soruyu şöyle de okuyabiliriz: $\arcsin \frac{1}{4}$ ifadesi sinüsü $\frac{1}{4}$ olan açıyı anlatmaktadır. Dolayısıyla sinüsü $\frac{1}{4}$ olan açının sinüsü sorulmaktadır.
Örnek
$\sin( 2\cdot \arcsin \frac{2}{3})$ ifadesinin değeri nedir?Çözüm
Bu soru bir önceki örnekle aynı değildir, burada fonksiyon ile tersinin birleşimi yoktur. $\arcsin \frac{2}{3}$ ifadesi, sinüsü $\frac{2}{3}$ olan açıya eşittir. Ancak bu açının değil, $2$ katının sinüsü sorulmakta.
\[ \arcsin \frac{2}{3} = x \Rightarrow \sin x = \frac{2}{3} \]
$\arcsin \frac{2}{3} = x$ eşitliğini soruda da kullanırsak:
\[\sin( 2\cdot \arcsin \frac{2}{3}) = \sin 2x\]
$\sin 2x$ sorulmakta ve $x$ açısının bir oranını bilmekteyiz. $\sin x = \frac{2}{3}$ ise dik üçgen yardımıyla $\cos x =\frac{\sqrt{5}}{3}$ çıkar.
\[ \sin 2x = 2 \sin x \cos x=2\cdot \frac{2}{3} \cdot \frac{\sqrt{5}}{3} = \frac{ 4\sqrt{5}}{9}\]
Ters Trigonometrik Fonksiyonların Grafikleri