Toplam Formülleri
İspatları bölüm sonunda yapılacak bu formüllerle, iki açının trigonometrik oranları biliniyorsa bunların toplamları ya da farklarının da değeri bulunabilir. Örneğin özel açılardan $30$ ve $45$ in trigonometrik oranlarını bildiğimizden, gerekirse $75$ veya $15$ in de değerlerini formülleri kullanarak bulabiliriz. Bunun yanında bu formüller, çözümlü örneklerde de görüleceği gibi geometri içeren bazı soru tiplerinde kullanılacaktır.[note1] sadece $\tan$ ı ezberleyip $\cot$ formüllerini bilmeden de hayata devam edilebilmektedir[/note]
\begin{align*}
\sin (x+y) &= \sin x \cos y + \cos x \sin y & \sin (x-y) &= \sin x \cos y - \cos x \sin y \\
\cos (x+y) &= \cos x \cos y - \sin x \sin y & \cos (x-y) &= \cos x \cos y + \sin x \sin y\\
\tan (x+y) &= \frac{\tan x + \tan y}{1-\tan x \tan y} & \cot (x+y) &= \frac{\cot x \cot y-1}{\cot x + \cot y}\\
\tan (x-y) &= \frac{\tan x - \tan y}{1+\tan x \tan y} &\cot (x-y) &= \frac{\cot x \cot y+1}{\cot x - \cot y}
\end{align*}
Çözümlü Örnekler
Örnek
$\sin 15^{\circ}$ nin değeri nedir?
Çözüm
$15$ özel iki açının, $45$ ve $30$ un farkıdır.
\[ \sin(x-y) = \sin x \cos y - \cos x \sin y \]
\begin{align*}
\sin(45-30) &= \sin 45\cos 30 - \cos 45 \sin 30 \\
&= \frac{\sqrt{2}}{2} \frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2} \frac{1}{2} \\
&= \frac{\sqrt{6} - \sqrt{2}}{4}
\end{align*}
Örnek
Bir $ABC$ üçgeninin iç açıları $A,B \text{ ve } C$ dir. $\tan A = \frac{1}{3}$ ve $\tan B= \frac{1}{4}$ olduğuna göre $\tan C$ değeri nedir?
Çözüm
$C$ açısı $180 - (A+B)$ dir. $\tan C = \tan (180 - (A+B))$ olur. $\tan (180 - \theta) = -\tan \theta $ olduğundan:
\begin{align*}
\tan (A+B) &= \frac{\tan A + \tan B}{1-\tan A \tan B} \\
&= \frac{\frac{1}{3} + \frac{1}{4}}{1-\frac{1}{3}\frac{1}{4}} \\
&= \frac{7}{11} \\
\end{align*}
\[ \tan C = \tan (180 - (A+B))=-\tan (A+B) = -\frac{7}{11} \]
Örnek
\[ \frac{\cos 30}{\cos 15} + \frac{\sin 30}{\sin 15}\] ifadesinin değeri nedir?
Çözüm
Paydaları eşitlediğimizde paya dikkat edelim:
\[ \frac{\cos 30 \sin 15}{\cos 15 \sin 15} + \frac{\sin 30\cos 15}{\sin 15 \cos 15}= \frac{\sin 45}{\frac{\sin 30}{2}} = 2\sqrt{2} \]
Örnek
Şekilde dört özdeş kare görülmektedir. Buna göre $\tan \widehat{ABC}$ değeri nedir?
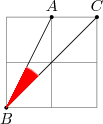
Çözüm
Bu sorularda bütün mesele sorulan açıyı, oranlarını bulabileceğimiz açıların toplamı ya da farkı olarak yazmaktır. Burada sorulan açı bir dik üçgen içinde değil. Ancak farkları $\widehat{ABC}$ olan ve dik üçgenler içinde bulunan (dolayısıyla $\tan$ larını bulabileceğimiz) iki açı vardır:
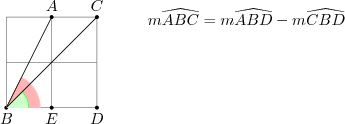
$m\widehat{ABD} = a$, $m\widehat{CBD} = b$ ve $m\widehat{ABC} = x$ olsun. $\tan a$ için $ABE$ dik üçgenini, $\tan b$ için de $CBD$ dik üçgenini kullanabiliriz:
\[ \tan a = \frac{|AE|}{|BE|}=2 \text{ ve } \tan b = \frac{|CD|}{|BD|}=1\]
\begin{align*}
\tan x = \tan (a-b) &= \frac{\tan a - \tan b}{1+\tan a \ tan b} \\
%\tan (a-b) &= \frac{\tan a - \tan b}{1+\tan a \ tan b}\\
&= \frac{2-1}{1+2} = \frac{1}{3}
\end{align*}
Örnek
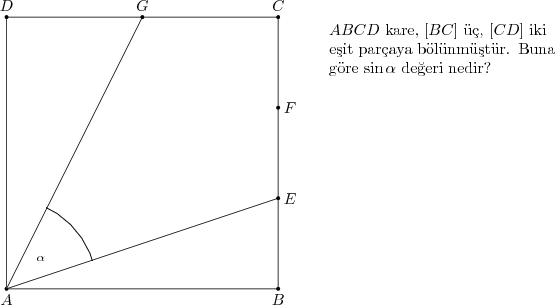
Çözüm
$\alpha$ bir dik üçgen içinde değil. Ancak toplamları $\alpha$ yı $90^{\circ}$ a tamamlayan $\widehat{DAG}$ ve $\widehat{EAB}$ açılarının oranları, içinde bulundukları dik üçgenlerden çıkar.
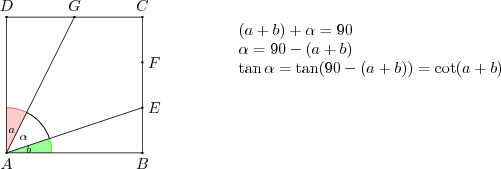
$m\widehat{GAD}=a$ ve $m\widehat{EAB} = b$ olsun.
\begin{align*}
\tan a &= \frac{|GD|}{|AD|}= \frac{1}{2} & \tan b &= \frac{|EB|}{|AB|}=\frac{1}{3}
\end{align*}
\[ \tan (a+b) = \frac{\tan a + \tan b}{1-\tan a \tan b}= 1\]
$\tan (a+b) = 1$ ise $\cot(a+b) = 1$ dir. Dolayısıyla $\tan \alpha = 1$ dir. $\tan$ değerini bildiğimiz bir açının $\sin$ değeri için bir dik üçgen çizmek yeterlidir. Ancak bu soruda buna da gerek yok, $\tan \alpha = 1$ ise $\alpha = 45^{\circ}$ dir ve $\sin \alpha = \frac{\sqrt{2}}{2}$ olur.[note2] Dikkat edilirse $\sin \alpha$ sorulduğu halde $\tan \alpha$ yı bulmaya çalıştık. $\tan$ formülü çoğu durumda daha pratiktir ve işlem hatası şansını azaltır. Örneğin bu durumda $a$ ve $b$ nin sinüs kosinüs değerleri için dik üçgenlerde hipotenüs hesaplamamız gerekiyordu.[/note]
Toplam Formülleri İspatı
Birim çemberde $x$ kadar dönerek bir $C$ noktasına, $y$ kadar dönerek bir $B$ noktasına varalım. Bu noktaların koordinatları şekilde görüldüğü gibi olacaktır. $C$ den düşey ve $B$ den de yatay çizerek $CBD$ dik üçgenini oluşturalım. İki açının farkı $x-y=\widehat{COB}$ dir.
Öte yandan başka bir birim çemberde bu fark kadar, yani $x-y$ dönelim ve $E$ noktasını bulalım.
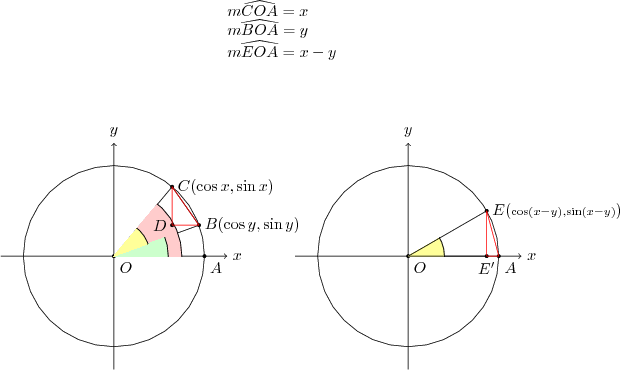
İspatın temeli $COB$ üçgeni ile $EOA$ üçgeninin eşliğine dayanır. İki üçgen de ikizkenardır ve ikizkenarlar birim çemberin yarıçapı kadardır. Bu kenarlar arası açı da aynı olduğundan
\[ |CB|=|EA| \]
Tüm yapacağımız, oluşturduğumuz dik üçgenlerden pisagor kullanarak $CB$ ve $EA$ nın uzunluklarını yazmak ve eşitlemek.
$BCD$ dik üçgeni için:
\begin{align*}
|BC|^2 &= |BD|^2 + |CD|^2 \\
&=(\cos y - \cos x)^2 + (\sin x - \sin y)^2\\
&= \cos^2 y - 2\cos y \cos x + \cos^2 x + \sin^2 x - 2\sin x \sin y + \sin^2 y\\
&= \cos^2 y + \sin^2 y + \cos^2 x + \sin^2 x -2(\cos x \cos y + \sin x \sin y)\\
&= 2-2(\cos x \cos y + \sin x \sin y)\\
\end{align*}
$EE'A$ dik üçgeni için:
\begin{align*}
|EA|^2 &= |E'A|^2 + |EE'|^2 \\
&=(1- \cos (x-y))^2 + (\sin (x - y))^2\\
&= 1 - 2\cos (x-y) + \cos^2 (x-y) + \sin^2 (x - y)\\
&= 2-2\cos (x-y)\\
\end{align*}
$|BC|=|EA|$ olduğundan
\begin{align*}
2-2(\cos x \cos y + \sin x \sin y) &= 2-2\cos (x-y) \\
\cos x \cos y + \sin x \sin y &= \cos (x-y)
\end{align*}
Böylece toplam formüllerinden $\cos(x-y)$ yi çıkarmış olduk. Bu formülü diğer formüllerin çıkarımında kullanacağız. Örneğin $y$ yerine $-y$ yazdığımızı düşünelim:[note3] $\cos(-x)=\cos x$ ve $\sin (-x)=-\sin x$ idi. [/note]
\begin{align*}
\cos (x+y) &= \cos x \cos (-y) + \sin x \sin (-y) \\
\cos (x+y) &= \cos x \cos y - \sin x \sin y
\end{align*}
$\cos (x-y)$ de $x$ yerine $90-x$ yazarsak
\begin{align*} \cos (90-x-y) &= \cos ([90-x]-y)) & \cos(90-x-y )&= \cos(90-[x+y]) \\
&=\cos (90-x)\cos y + \sin (90-x)\sin y & &=\sin(x+y)\\
&=\sin x \cos y + \cos x \sin y\\
\end{align*}
$\sin(x+y)=\sin x \cos y + \cos x \sin y$ özdeşliğini elde ettik. $y$ yerine $-y$ yazdığımızda da $\sin(x-y)$ elde edilir.
